Resolver

ENUNCIADO. Resolver las siguientes ecuaciones:
a) $2x-1=4-7x$
b) $3\,(1-x)=4+5\,x$

SOLUCIÓN.
a)
$2x-1=4-7x$
  $2x+7x=4+1$
    $9x=5$
      $x=\dfrac{5}{9}$

b)
$3\,(1-x)=4+5\,x$
  $3 \cdot 1-3\,x=4+5\,x$
    $3-3\,x=4+5\,x$
      $3-4=5\,x+3\,x$
        $-1=8\,x$
          $x=\dfrac{-1}{8}=-\dfrac{1}{8}$
$\square$

Expresar en el lenguaje del álgebra

ENUNCIADO. Escribir las expresiones algebraicas:
a) El cuadrado de la diferencia de dos números
b) El inverso de un número
c) El opuesto de un número
d) El área de un círculo de radio dado
e) La longitud de una circunferencia de radio dado

SOLUCIÓN.
a) $(x-y)^2$
b) $\dfrac{1}{x}$
c) $-x$
d) $\pi \, r^2$
e) $2\,\pi\,r$
$\square$

Dividir los polinomios ...

ENUNCIADO. Calcular el polinomio cociente y el polinomio resto que corresponden a la siguiente división de polinomios: $$(4\,x^3-5\,x+1) \div 3\,x^2$$
y comprobar que se cumple el teorema de la división ( de polinomios ).

SOLUCIÓN.

Comprobación:

$\square$

Hallar el valor numérico de los polinomios, dados los siguientes valores de la variable

ENUNCIADO. Hallar el valor numérico del polinomio $$A(x)=7\,x^2-x+5\,x+5$$ para los siguientes valores de la variable $x$:
a) $x=-1$
b) $x=2$

SOLUCIÓN.
a)
$P(-1)=7\cdot (-1)^2-(-1)+5\cdot (-1)+5$
      $=7\cdot 1+1-5+5$
        $=7+1-5+5$
          $=8-5+5$
            $=8$

b)
$P(2)=7\cdot 2^2-2+5\cdot 2+5$
      $=7\cdot 4-2+10+5$
        $=28-2+10+5$
          $=26+10+5$
            $=36+5$
              $=41$

$\square$

Operar los siguientes polinomios

ENUNCIADO. Considérense los polinomios $$P(x)=8\,x^3+x^2-4\,x+5$$ $$Q(x)=3\,x^2-x^2+x-1$$ Realizar las siguientes operaciones con polinomios y decir cuál es el grado de los polinomios resultantes:
a) $2\,P(x)$
b) $-3\,Q(x)$
c) $P(x)+Q(x)$
d) $P(x)-Q(x)$
e) $Q(x)-P(x)$
f) $P(x)\cdot Q(x)$

SOLUCIÓN.
a)
$2\,P(x)=2\cdot ( 8\,x^3+x^2-4\,x+5 )= 2\cdot 8 \,x ^3+2\,x^2-2\cdot 4\,x+2\cdot 5=$
    $=16 \,x ^3+2\,x^2-8\,x+10$. El grado del polinomio resultante es $3$.

b)
$(-3)\,P(x)=(-3)\cdot ( 8\,x^3+x^2-4\,x+5 )=$
  $=(-3)\cdot 8 \,x ^3+(-3)\cdot x^2+(-3)(-4\,x)+(-3)\cdot 5=$
    $=-24 \,x ^3-3\,x^2+12\,x-15. $El grado del polinomio resultante es $3$.

c)
$(8\,x^3+x^2-4\,x+5)+(3\,x^2-x^2+x-1)=8\,x^3+4\,x^2-3\,x+4$. El grado del polinomio resultante es $3$.

d)
$(8\,x^3+x^2-4\,x+5)-(3\,x^2-x^2+x-1)=8\,x^3+x^2-3\,x^2-4\,x-x+5-(-1)=$
  $=8\,x^3-2\,x^2-5\,x+6$. El grado del polinomio resultante es $3$.

e)
$Q(x)-P(x)=-(P(x)-Q(x))=-(8\,x^3-2\,x^2-5\,x+6)=-8\,x^3+2\,x^2+5\,x-6$. El grado del polinomio resultante es $3$.

f)
$(8\,x^3+x^2-4\,x+5)\cdot (3\,x^2-x^2+x-1)=(8\,x^3+x^2-4\,x+5)\cdot (2\,x^2+x-1)=$
  $=16\,x^5+2x^4-8x^3-10x^2+$
    $+(-8)x^4-x^3+4x^2-5x+$
      $+(-8)x^3-x^2+4x-5=$
        $16x^5-6x^4-17x^3+13x^2-x-5$. El grado del polinomio producto es igual a la suma de los grados de los polinomios factores, esto es, el grado es $5$ ( como, además, podemos apreciar al observar el término de mayor grado ).
$\square$

Plantear mediante el álgebra y resolver

ENUNCIADO. En una librería, Ana compra un libro con la tercera parte de su dinero y un cómic con las dos terceras partes de lo que le quedaba. Al salir de la librería tenía $12$ euros. ¿Cuánto dinero tenía Ana antes de hacer su compra ?.

SOLUCIÓN.
Llamemos $x$ a la cantidad de dinero que tenía Ana antes de entrar en la librería. Entonces, $$x=\dfrac{x}{3}+\dfrac{2}{3}\,(x-\dfrac{x}{3})+12$$
Resolviendo esta ecuación:
$x=\dfrac{x}{3}+\dfrac{2}{3}\,(x-\dfrac{x}{3})+12$
  $x=\dfrac{x}{3}+\dfrac{2}{3}\cdot \dfrac{2}{3}\,x+12$
    $x=\dfrac{x}{3}+\dfrac{4}{9}\,x+12$
      $9x=9\cdot \dfrac{x}{3}+9\cdot \dfrac{4}{9}\,x+9\cdot 12$
        $9x=3x+4x+108$
          $9x-3x-4x=108$
            $2x=108$
              $x=108/2=54\;\text{euros}$
$\square$

Plantear y resolver

ENUNCIADO. El largo de un marco rectangular es el doble del ancho. ¿ Cuáles son sus dimensiones si el perímetro mide $30$ centímetros ?

SOLUCIÓN.
Denotemos por $x$ el ancho del marco, entonces
$$2\,(2x+x)=30$$
Resolvamos la ecuación:
$2\,(2x+x)=30$
  $2x+x=15$
    $3x=15$
      $x=15/3=5 \; \text{cm}$
luego el largo es igual a $2x=2\cdot 5=10\;\text{cm}$
$\square$

Platear y resolver el siguiente problema

ENUNCIADO. Si al doble de un número se le resta su mitad resulta el número $54$. ¿ De qué número estamos hablando ?

SOLUCIÓN.
Denotemos por $x$ el número pedido. Entonces, $$2x-\dfrac{x}{2}=54$$
Resolvamos, ahora, la ecuación:
$2x-\dfrac{x}{2}=54$
  $2\cdot 2x-2\cdot \dfrac{x}{2}=2\cdot 54$
    $4x-x=108$
      $3x=108$
        $x=\dfrac{108}{3}$
          $x=36$
$\square$

Resolver las ecuaciones de segundo grado

ENUNCIADO. Resolver las siguientes ecuaciones de segundo grado:
a) $x^2+4\,x-5=0$
b) $(x+1)(x-2)=0$

SOLUCIÓN.
a)
$x^2+4\,x-5=0$
  $1\cdot x^2+4\,x+(-5)=0$. Por tanto, en $ax^2+bx+c=0$, los valores de los coeficientes son $a=1$; $b=4$ y $c=-5$. Así, $$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}=\dfrac{-4\pm \sqrt{4^2-4\cdot 1\cdot (-5)}}{2\cdot 1}=\dfrac{-4\pm \sqrt{36}}{2}=\dfrac{-4\pm 6}{2}$$
luego $x=\left\{\begin{matrix}\dfrac{-4+6}{2}=\dfrac{2}{2}=1\\\text{ó}\\\dfrac{-4-6}{2}=\dfrac{-10}{2}=-5\end{matrix}\right.$
Resumiendo, la solución de la ecuación pedida viene dada por el conjunto de números $\{-5\,,\,1\}$

b)
$(x+1)(x-2)=0$
Esta igualdad a $0$ sólo es posible si $x+1=0$, y, por tanto, si $x=-1$; o bien, si $x-2=0$, y, por tanto, si $x=2$. En conclusión, la solución de la ecuación pedida viene dada por el conjunto de números $\{-1\,,\,2\}$
$\square$

Resolver las ecuaciones de primer grado

ENUNCIADO. Resolver las siguientes ecuaciones de primer grado:
a) $2\,x+5=1-3\,x$
b) $\dfrac{x+1}{3}-\dfrac{5}{18}=\dfrac{x+1}{12}$

SOLUCIÓN.
a)
$2\,x+5=1-3\,x$
  $2\,x+4\,x=1-5$
    $6\,x=-4$
      $x=\dfrac{-4}{6}$
        $x=-\dfrac{4}{6}$
          $x=-\dfrac{2}{3}$

b)
$\dfrac{x+1}{3}-\dfrac{5}{18}=\dfrac{x+1}{12}$
Multiplicando en ambos miembros por $\text{m.c.m}(3,18,12)=\text{m.c.m}(3,2\cdot 3^2,2^2\cdot 3)=2^2\cdot 3^2=36$, obtenemos la siguiente ecuación equivalente
  $36\cdot \dfrac{x+1}{3}-36\cdot\dfrac{5}{18}=36\cdot\dfrac{x+1}{12}$
    $12\cdot(x+1)-2\cdot 5=3\cdot (x+1)$
      $12\,x+12-10=3\,x+3$
        $12\,x-3\,x=3-12+10$
          $9\,x=1$
            $x=\dfrac{1}{9}$
$\square$

Hallar el máximo común divisor y el mínimo común múltiplo de los siguientes números naturales

ENUNCIADO. Considerar los números naturales $42$, $72$ y $84$. Se pide:
a) el \textit{máximo común divisor} de dichos números
b) el \textit{mínimo común múltiplo} de dichos números

SOLUCIÓN. Descomponiendo en factores cada uno de los números: $$42=2\cdot 3 \cdot 7$$ $$72=2^3\cdot 3^2$$ $$84=2^2\cdot 3 \cdot 7$$
Por consiguiente $$\text{a)} \quad \text{m.c.d}(42\,,\,72\,,\,84)=\text{m.c.d}(2\cdot 3 \cdot 7\,,\,2^3\cdot 3^2\,,\,82^2\cdot 3 \cdot 7)=2\cdot 3=6$$ $$\text{b)} \quad\text{m.c.m}(42\,,\,72\,,\,84)=\text{m.c.m}(2\cdot 3 \cdot 7\,,\,2^3\cdot 3^2\,,\,82^2\cdot 3 \cdot 7)=2^3\cdot 3^2 \cdot 7=504$$
$\square$

[autoría]

Fracciones equivalentes y no-equivalentes

ENUNCIADO. ¿ Son equivalentes las fracciones $\dfrac{111}{112}$ y $\dfrac{112}{113}$ ?.
Razónese la respuesta.

SOLUCIÓN. Para que dos fracciones sean equivalentes es necesario que el producto de medios sea igual al producto de extremos. Sin embargo es evidente que $111 \cdot 113 \neq 112 \cdot 112 $, luego las fracciones pedidas no son equivalentes, y se escribe $$\dfrac{111}{112} \neq \dfrac{112}{113}$$
$\square$

[autoría]

Simplificación de fracciones

ENUNCIADO. Calcular la fracción irreducible resultante:
a) $\dfrac{2}{3}-\dfrac{5}{18}+\dfrac{1}{12}$
b) $\dfrac{7}{4}\cdot \dfrac{8}{14}$
c) $\dfrac{9}{5}\div \dfrac{81}{125}$

SOLUCIÓN.

a)

$\dfrac{2}{3}-\dfrac{5}{18}+\dfrac{1}{12}=$

  $=\dfrac{2\cdot (36\div 3)}{36}-\dfrac{5 \cdot ( 36 \div 18) }{36}+\dfrac{1\cdot ( 36\div 12)}{36}$ ( reduciendo a común denominador; el mínimo común múltiplo de los denominadores es $36$.)

    $=\dfrac{24}{36}-\dfrac{10 }{36}+\dfrac{3}{36}$

      $=\dfrac{24}{36}+\dfrac{(-10) }{36}+\dfrac{3}{36}$

        $=\dfrac{24+(-10)+3}{36}$

          $=\dfrac{24+(-10)+3}{36}$

            $=\dfrac{17}{36}$

b)

$\dfrac{7}{4}\cdot \dfrac{8}{14}=$

  $=\dfrac{7 \cdot 8}{4 \cdot 14}$

    $=\dfrac{8 \cdot 7}{4 \cdot 14}$

      $=\dfrac{8}{4}\cdot \dfrac{7}{14}$

        $=2\cdot \dfrac{1}{2}$

          $=1$

c)

$\dfrac{9}{5}\div \dfrac{81}{125}=$

  $=\dfrac{9}{5} \cdot \text{inverso}\left( \dfrac{81}{125}\right)$

    $=\dfrac{9}{5}\div \dfrac{125}{81}$

    $=\dfrac{9\cdot 125}{5 \cdot 81}$

      $=\dfrac{125}{5}\cdot \dfrac{9}{81}$

        $=25\cdot \dfrac{1}{9}$

          $=\dfrac{25}{9}$

$\square$

[autoría]

Cálculo de radicales

ENUNCIADO. El área de un cuadrado mide $169 \; \text{m}^2$, ¿ cuánto mide su perímetro ?.

SOLUCIÓN. Denotemos por $x$ la longitud del lado del cuadrado, entonces $x^2=169$, luego $x=\sqrt{169}=13\; \text{m}$. Y como el perímetro, $P$, es $4x$, encontramos que $P=4\cdot 13 = 52\;\text{m}$
$\square$

[autoría]

Cálculo de radicales

ENUNCIADO. Calcular el siguiente radical ( sin utilizar la calculadora científica ), dando como resultado el menor número natural más próximo ( a dicho radical ) así como el número natural que representa el resto de la operación $$\sqrt{2449}$$

SOLUCIÓN. Observemos que $50^2=2500 \succ 2449$ y que $49^2=2401 \prec 2449$, luego podemos decir que $\sqrt{2449}$ es igual a $49$ con resto $2449-2401=48$
$\square$

[autoría]

Fracciones propias e impropias

ENUNCIADO. Expresar la fracción impropia $\dfrac{7}{5}$ en forma mixta, esto es, como la suma del número entero menor y más próximo a la fracción y una fracción propia.

SOLUCIÓN. De la división entera $7\div 5$ obtenemos $1$ de cociente y $2$ de resto, entonces $7=5\cdot 1 +2$; así que, multiplicando por $\dfrac{1}{5}$ en cada miembro de esta igualdad, llegamos a $\dfrac{1}{5}\cdot 7=\dfrac{1}{5}\cdot 5\cdot 1 +\dfrac{1}{5}\cdot 2$, esto es (simplificando), $$\dfrac{7}{5}=1+\dfrac{2}{5}$$
$\square$

[autoría]

Ordenación de fracciones

ENUNCIADO. Ordenar de menor a mayor las siguientes fracciones, sin recurrir a sus expresiones decimales:
$$\lbrace \,\dfrac{3}{4}\,,\,\dfrac{2}{3}\,,\,\dfrac{4}{3}\,,\,\dfrac{4}{5}\,,\,\dfrac{3}{2} \, \rbrace$$

ENUNCIADO. Para comparar las fracciones, procedemos a reducirlas a común denominador ( encontramos una fracción equivalente, a cada una, que tenga el mismo denominador ), de este modo, bastará ordenar los nuevos numeradores para que dicho orden determine el orden de las fracciones respectivas. Calculemos, pues, el mínimo común múltiplo de los denominadores de las fracciones dadas $$\text{m.c.m}(2,3,4,5)=60$$

Así,

$\dfrac{3}{4}=\dfrac{3\cdot 15}{60}=\dfrac{45}{60}$

$\dfrac{2}{3}=\dfrac{2\cdot 20}{60}=\dfrac{40}{60}$

$\dfrac{4}{3}=\dfrac{4\cdot 20}{60}=\dfrac{80}{60}$

$\dfrac{4}{5}=\dfrac{4\cdot 12}{60}=\dfrac{48}{60}$

$\dfrac{3}{2}=\dfrac{3\cdot 30}{60}=\dfrac{90}{60}$

Por tanto, $$\dfrac{2}{3} \prec \dfrac{3}{4} \prec \dfrac{4}{5} \prec \dfrac{4}{3} \prec \dfrac{3}{2} $$

$\square$

[autoría]

División entera

ENUNCIADO. Calcular el resto y el cociente de la siguiente división entera $$1258 \div 145$$

SOLUCIÓN. $\text{cociente}(1258 \div 145)=8$, ya que $8 \cdot 145 \prec 1258$ y $(8+1) \cdot 145 \succ 1258$; entonces $\text{resto}(1258 \div 145)=1258-8\cdot 145=98$
$\square$

[autoría]

Expresión decimal de una fracción

ENUNCIADO. Expresar las siguientes fracciones ( de números enteros ) en forma decimal y decir si se trata de un número decimal exacto, periódico puro, o bien periódico mixto:
a) $\dfrac{4}{9}$
b) $\dfrac{8}{11}$
c) $\dfrac{6}{13}$
d) $\dfrac{97}{90}$

SOLUCIÓN.

Realizando la división decimal del numerador entre el denominador, de cada fracción:

a) $\dfrac{4}{9}=0,\overline{4}$   ( número decimal periódico puro )

b) $\dfrac{8}{11}=0,\overline{561538}$   ( número decimal periódico puro )

d) $\dfrac{97}{90}=1,0\,\overline{7}$   ( número decimal periódico mixto )

$\square$

[autoría]

Operaciones con números enteros

ENUNCIADO. Efectuar las siguientes operaciones con números:
a) $1-\text{opuesto}(3)+2-|3|$
b) $1-(-1)-\text{opuesto}(1)$
c) $(4+|-1|)^3 \div 25-1$
d) $2+2^5 \div 2^3-2^2 $
e) $3^2 \cdot 3^3 \cdot 5^0$
f) $\left((-2)^5\right)^2$
g) $\left(2+3\right)^3$
h) $\sqrt{121 \cdot 625}$

SOLUCIÓN.
a)

$1-\text{opuesto}(3)+2-|3|=$

  $=1-(-3)+2-3$

    $=1+\text{opuesto}(-3)+2-3$

      $=1+3+2-3$

        $=3$

b)

$1-(-1)-\text{opuesto}(1)=$

  $=1+\text{opuesto}(-1)-(-1)$

    $=1+1+\text{opuesto}(-1)$

      $=1+1+1$

        $=3$

c)

$(4+|-1|)^3 \div 25-1=$

  $=(4+1)^3 \div 25 -1$

    $=5^3 \div 25 -1$

      $=125 \div 25 -1$

        $=5 -1$

          $=4$

d)

$2+2^5 \div 2^3-2^2=$

  $=2+2^{5-3}-2^2$

    $=2+2^{2}-2^2$

      $=2+0$

        $=2$

e)

$3^2 \cdot 3^3 \cdot 5^0=$

  $=3^2 \cdot 3^3 \cdot 1$

    $=9 \cdot 27 \cdot 1$

      $=243$

f)

$\left((-2)^5\right)^2=$

  $=\left(-2^5\right)^2$

    $=\left((-1)\cdot 2^5\right)^2$

    $=(-1)^2 \cdot \left(2^5\right)^2$

      $=(+1) \cdot {2^5 \cdot 2}$

        $=2^{10}$

          $=1024$

g)

$\left(2+3\right)^3=$

  $=5^3$

    $=125$

h)

$\sqrt{121 \cdot 625}=$

  $=\sqrt{121} \cdot \sqrt{625}$

    $=11 \cdot 25$

      $=275$

$\square$

[autoría]

Fotografía de un número hexagonal y triangular

Madrid, Octubre de 2015

[número hexagonal] que también es triangular.

[autoría]

Fotografía de un número triangular

Madrid, Octubre de 1015

[ número triangular ]

[autoría]

Hemos recorrido tres cuartas partes de ...

ENUNCIADO. Hemos recorrido tres cuartas partes de un camino, y aún nos quedan $2$ quilómetros para llegar. Se pide:
a) ¿ Qué fracción del camino nos queda por recorrer ?
b) ¿ Qué longitud de camino hemos recorrido ?
c) ¿ Cuál es la longitud total del camino ?

SOLUCIÓN.
a) Si hemos recorrido tres cuartas partes del camino, nos queda por recorrer $\dfrac{4}{4}-\dfrac{3}{4}=\dfrac{1}{4}$ del camino
c) Denotando por $x$ la longitud del camino, debe cumplirse la siguiente equivalencia $$\dfrac{1}{4}=\dfrac{2}{x}$$ con lo cual $$1 \cdot x = 2 \cdot 4$$ esto es $$x=8\,\text{km}$$
b) Como el camino tiene una longitud de $8 \, \text{km}$ y faltan $2\, \text{km}$ por recorrer, hemos recorrido ya $8-2=6\, \text{km}$
$\square$

[autoría]

El número de páginas de un libro ...

ENUNCIADO. El número de páginas de un libro es igual a un número cuadrado más $13$. Si se le suma $20$ ( al número de páginas de este libro ), se obtiene el número cuadrado mayor y más próximo al número cuadrado del que hablábamos. ¿ Cuántas páginas tiene el libro ?.

SOLUCIÓN. Denotemos por $x$ al número cuadrado del que se habla en la primera frase. Entonces cabe plantear la siguiente igualdad:
$$(x^2+13)+20=(x+1)^2$$ es decir $$x^2+33=x^2+2\,x+1$$ simplificando $$33=2\,x+1$$ esto es $$32=2\,x$$ luego $x=16$ y, por tanto, el número de páginas del libro es $16^2+13=256+13=269$.
$\square$

[autoría]

¿ Qué longitud de hilo se necesita para ... ?

ENUNCIADO. Se quiere rodear una parcela cuadrada e $1225 \, \text{m}^2$ de superficie con un hilo. ¿ Cuántos metros de hilo necesitamos ?

SOLUCIÓN. Denotemos por $x$ la longitud de un lado de la parcela cuadrada, entonces $1125 = x^2$, luego $=\sqrt{1225}=35 \, \text{m}$; así, el perímetro, que es $4\,x$, es $4 \cdot 35 = 140 \, \text{m}$
$\square$

[autoría]

Hallar el menor número entero positivo tal que ...

ENUNCIADO. Hallar el menor número entero positivo que hay que restar a $8561$ para obtener un número cuadrado.

SOLUCIÓN. Como $91^2=8281 \prec 8561$, probamos con $92$; $92^2=8464 \prec 8561$; sin embargo $93^2=8649 \succ 8561$, luego el número cuadrado mayor que $8561$ y más cercano al mismo es $8464$. Por consiguiente, debemos encontrar $x$ tal que $8561-x=8464$, esto es, $x=8561-8464$, que es igual a 97. $\square$

[autoría]

Expresar en forma de suma de términos con potencias de diez

ENUNCIADO. Expresar el número $8495,716$ como una suma de términos con potencias de diez.

SOLUCIÓN. La cantidad dada significa, en forma literal, lo siguiente: ocho millares y cuatro centenas y nueve decenas y cinco unidades y siete décimas y una centésima y seis milésimas ( de acuerdo con el significado de la notación posicional del sistema decimal ), luego podemos escribir lo que nos piden de la forma $$8495,716=8\cdot 10^3+4\cdot 10^2+9\cdot 10+5+7\cdot 10^{-1}+1 \cdot 10^{-2}+6\cdot 10^{-3}$$
$\square$

[autoría]

Determinar el menor número entero tal que ...

ENUNCIADO. Determinar el menor número entero más próximo a $\sqrt{29}$ y el resto correspondiente.

SOLUCIÓN. Com $5^2=25 \prec 29$ y $6^2=36 \succ 29$, el número pedido es $5$, y el resto es igual a $29-5^2=4$.

Nota: Podemos acotar la raíz cuadrada de $29$ entre los números enteros $5$ y $6$. Y lo escribimos de la siguiente forma $5 \prec \sqrt{29} \prec 6$

$\square$

[autoría]

Relación entre el máximo común divisor y mínimo común múltiplo de dos números enteros

ENUNCIADO:
Sabiendo que $\text{m.c.d}(|15|,|-10|)=5$ ( es decir, $\text{m.c.d}(15,-10)=\pm \,5$ ) , determinar $\text{m.c.m}(15,-10)$

SOLUCIÓN:
Sabemos que dados dos números enteros $m$ y $n$, se cumple la siguiente propiedad: $$\text{m.c.d}(|m|,|n|) \cdot \text{m.c.m}(|m|,|n|)=|m|\cdot |n|$$ entoces podemos escribir $$5 \cdot \text{m.c.m}(|15|,|-10|) = 15 \cdot 10$$ de donde, despejando $\text{m.c.m}(|15|,|-10|)$ obtenemos $$\text{m.c.m}(|15|,|-10|)=\dfrac{|15| \cdot |-10|}{5} $$ esto es $$\text{m.c.m}(|15|,|-10|)=\dfrac{150}{5}=30 $$ luego deducimos que $$\text{m.c.m}(15,-10)=\pm \, 30$$
$\square$

[autoría]

Realizar la siguiente división con números enteros ...

ENUNCIADO:
Hallar el cociente y el resto de la división entera $-15 \div 7$

SOLUCIÓN:
El teorema de la división entera dice que dados dos números enteros cualesquiera $D$ y $d$, a los que denominamos dividendo y divisor, respectivamente, entonces podemos encontrar otros dos números enteros, $c$ y $r$, a los que denominamos cociente y resto de la división, que cumple las siguientes condiciones:
i) $D=d\cdot c +r$
y
ii) $0 \le r \prec |d|$ ( el resto es mayor o igual que cero y menor que el valor absoluto del divisor )

Procedemos a encontrar los números $c$ y $r$ que cumplen estas condiciones, siendo $D:=-15$ y $d:=7$. Para el cociente, probemos con un número tal que multiplicado por el divisor $7$ nos dé un número que se aproxime al dividendo, que es $-15$. Por la regla de los signos del producto, sabemos que debe ser negativo ( ya que el dividendo es negativo y el divisor positivo ); así que, ensayemos el número $c \rightarrow -2$. Como $-2 \cdot 7 = -14 \succ -15$, el resto de la división seria $-15-(7\cdot (-2)=-1\prec 0$, luego al ser el resto negativo se incumple la segunda condición y por tanto no podemos admitir $-2$ como cociente, así que pasemos al siguiente número entero más pequeño, es decir hagamos $c \rightarrow -3$. Como $-3 \cdot 7 = -21$, y el resto es $-15-(7\cdot (-3)=6\succ 0$ ( se cumple la segunda condición ), concluimos que $c=-3$, luego el resto de la división debe ser $-15-(-21)=-14+21=6$, es decir $r=6$.

Sólo nos falta comprobar que, con estos valores del cociente y resto, se cumple también la primera condición; en efecto: $-15=7\cdot (-3)+6$. Por consiguiente, podemos afirmar que el cociente y el resto pedidos son: $c=-3$ y $r=7$

$\square$

Hallar el máximo común divisor de los números naturales $64$ y $24$, empleando el método de Euclides

ENUNCIADO:
Determinar el máximo común divisor de $64$ y $24$ empleando el método de las divisiones sucesivas o método de Euclides.

SOLUCIÓN:
Este método se basa en hallar el cociente y el resto de la división de números naturales [ lógicamente, entre el mayor de los dos números ( $D_1$ ) y el menor ($d_1$ ) ]; si el resto de dicha división es $0$, el máximo común divisor pedido es igual al menor de los dos ( el divisor ), y hemos terminado; si no es así, hacemos otra división, donde el nuevo dividendo es ahora el antiguo divisor y el nuevo divisor el antiguo resto, haciendo la misma comprobación ( si el nuevo resto es cero, el máximo común divisor de los dos números pedidos es el divisor de dicha división ); en caso contrario, volvemos a repetir el mismo paso ( otra división, asignando nuevo dividendo y nuevo divisor ) y, así, una y otra vez, hasta llegar a una división cuyo resto sea cero, de lo cual concluiremos que el $\text{m.c.d}(64,24)$ ha de ser igual al divisor de esta última división, y terminamos.

Bien, en el caso del enunciado:

$D_1=64$ y $d_1=24$ y realizamos la división
$$64 \div 24 \rightarrow \left\{\begin{matrix}
c_1=2 \\
\\
\text{y}
\\
r_1=16 \neq 0 \rightarrow \left\{\begin{matrix}
D_2:=d_1=24 \\
\\
d_2:=r_1=16
\end{matrix}\right.
\end{matrix}\right.$$

como el resto no es cero, continuamos ...

$D_2=24$ y $d_2=16$ y realizamos la división:
$$24 \div 16 \rightarrow \left\{\begin{matrix}
c_2=1 \\
\\
\text{y}
\\
r_2=8 \neq 0 \rightarrow \left\{\begin{matrix}
D_3:=d_2=16 \\
\\
d_3:=r_2=8
\end{matrix}\right.
\end{matrix}\right.$$

como el resto no es cero, continuamos ...

$D_3=16$ y $d_3=8$ y realizamos la división:
$$16 \div 8 \rightarrow \left\{\begin{matrix}
c_3=2 \\
\\
\text{y}
\\
r_2=0
\end{matrix}\right.$$

y como el resto ( en este paso ) es cero , concluimos que $\text{m.c.d.}(64,24)=d_3=8$, y hemos terminado.

OBSERVACIÓN: Teniendo en cuenta que todo número natural es también un número entero, si interpretamos los números naturales dados como números enteros, debemos decir que el $\text{m.c.d.}(64,24)$ no es tan solo $8$ sino también $-8$; en efecto, al ser el resto de la división $64 \div (-8)$ ( ahora, división entera ) igual a $0$, es claro que $-8$ también es divisor de $64$; y, lo mismo, sucede con respecto a la división de $24$ entre $-8$.

$\square$

División de números naturales

ENUNCIADO:
Calcular el resto, $r$, de la división del número natural $15$ ( dividendo ) entre el número natural $7$ ( divisor ) mediante el procedimiento de las restas sucesivas.

SOLUCIÓN:
Procedamos a restar el divisor ( $7$ ) del dividendo ( $15$ ), luego sustituimos el dividendo por el resultado de la resta y volvemos a restar el divisor de dicho número, y, así, hasta llegar a una resta cuyo resultado sea menor que el divisor; el resultado de esta última resta ha de ser el valor del resto de la división. Lo abreviaremos con la siguiente notación:

Partimos de
$$[15 \quad ; \quad 7]$$
y restamos sucesivamente
$$\text{i)} \quad [15-7=8 \quad ; \quad 7]$$
$$\text{ii)} \quad [8-7=1 \prec 7 \quad ; \quad 7] $$
y acabamos ( ya que el valor de la resta, $1$, es menor que el del divisor ), luego deducimos que $$r=1$$

Comprobación:
Se cumple el teorema de la división con números naturales. En efecto: como hemos realizado dos pasos en dicho proceso, el cociente de la división es $c=2$; y como el resto hallado es $r=1$, se comprueba que se cumple la igualdad $15 = 7 \cdot 2 + 1$, y, además $r=1 \prec 7$ ( el resto es mayor que el divisor ).

$\square$

[autoría]

Realizar las siguientes operaciones, donde interviene el valor absoluto y el opuesto de un número

ENUNCIADO:
Calcular:
a) $|(-3)|-(-3)$

b) $\text{opuesto}(-3)-(-3)$

c) $|3|-(+3)$

d) $\text{opuesto}(+3)-(+3)$

e) $|(-3)|-(-3)$

f) f) $(+3)-|(+3)|$

g) $(-3)-|(-3)|$


SOLUCIÓN:
a) $|(-3)|-(-3)=(+3)+\text{opuesto}(-3)=(+3)+(+3)=+6$

b) $\text{opuesto}(-3)-(-3)=(+3)+\text{opuesto(-3)=(+3)+(+3)=+6}$

c) $|(+3)|-(+3)=(+3)+\text{opuesto}(+3)=(+3)+(-3)=0$

d) $\text{opuesto}(+3)-(+3)=(-3)+\text{opuesto}(+3)=(-3)+(-3)=-6$

e) $|(-3)|-(-3)=(+3)+\text{opuesto}(-3)=(+3)+(+3)=+6$

f) $(+3)-|(+3)|=(+3)-(+3)=(+3)+\text{opuesto}(+3)=(+3)+(-3)=0$

g) $(-3)-|(-3)|=(-3)-(+3)=(-3)+\text{opuesto}(+3)=(-3)+(-3)=-6$

$\square$

[autoría]

Resta de números enteros

ENUNCIADO:
Demostrar que la resta de dos números enteros no cumple la propiedad conmutativa. Ayuda: basta encontrar un contra-ejemplo.

SOLUCIÓN:
Supongamos que se cumple la propiedad conmutativa para la operación resta de números enteros, entonces, por un lado tenemos que $$(+2)-(+1)=(+2)+\text{opuesto}(+1)=+2+(-1)=+1$$ por otra parte $$(+1)-(+2)=(+1)+\text{opuesto}(+2)=(+1)+(-2)=-1$$ y como hemos supuesto que ambos resultados deben ser iguales, $+1 = -1$, lo cual es es absurdo, luego debemos negar lo que hemos supuesto al principio ( "la resta de dos números enteros es conmutativa " ), y, de ello concluimos que la resta de dos números enteros no es conmutativa, tal como queríamos demostrar.

$\square$

[autoría]

Resta de números enteros

ENUNCIADO:
Expresar las siguientes restas de números enteros mediante la combinación de la operación suma y el opuesto del sustraendo, y finalmente, calcular el resultado de dicha resta:
a) $(+5)-(+1)$
b) $(-1)-(-7)$
c) $(-11)-(+3)$

SOLUCIÓN:
a) $(+5)-(+1)=(+5)+\text{opuesto}(+1)=(+5)+(-1)=+4$
b) $(-1)-(-7)=(-1)+\text{opuesto}(-7)=(-1)+(+7)=+6$
c) $(-11)-(+3)=(-11)+\text{opuesto}(+3)=(-11)+(-3)=-14$

$\square$

[autoría]

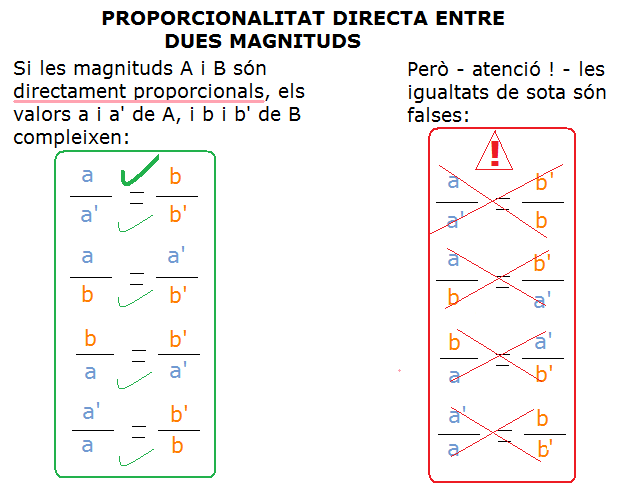
proporcionalidad simple y directa ...

Porcentajes ...

La suma de dos números naturales es ...

Enunciat:
La suma de dos nombres naturals és igual a $106$ i en dividir el més gran entre el més petit obtenim $2$ de quocient i $10$ de residu. Trobeu aquests nombres.

Resolució:
Considerant que $x > y$; de l'enunciat, podem plantejar el sistema d'equacions

$\left.\begin{matrix} x+y = 106 \\ x = 2y+10\\ \end{matrix}\right\}$

on la segona equació es refereix a la propietat fonamental de la divisió

dividend = divisor · quaciente + residu

Substituint l'expressió de $x$ de la segona equació en la primera trobem una equació amb una sola variable
$2y+10+y=106$
que equival a
$3y=96$
d'on trobem que
$y=32$

i, per tant, el valor de $x$ ha de ser igual (primera equació) a
$x=110-32$
és a dir
$x=78$

$\square$

Sistema decimal de numeración

La suma de los cuadrados de tres números naturales consecutivos es igual a la suma de los cuadrados de los dos siguientes números consecutivos. ¿ De qué números estamos hablando ?

Enunciat:
La suma dels quadrats de tres nombres naturals consecutius és igual a la suma dels quadrats dels dos següents. Quins nombres són ?

Resolució:
Anomenem $n$ al nombre més petit d'aquests tres; llavors, segons l'enuncitat, s'escau escriure la següent equació

$n^2+(n+1)^2+(n+2)^2=(n+3)^2+(n+4)^2$

desenvolupant els binomis al quadrat, i agrupant i ordenant els termes, trobem l'equació equivalent

$n^2-8n-20=0$

resolent-la, trobem dos valors com a solució:

$n_1=-2$ (que no és un nombre natural) i $n_2=10$

Tan sols el segon és solució del problema (ens demanen un nombre natural); per tant, els tres nombres naturals consecutius demanats són: 10, 11 i 12

$\square$

Proporcionalidad inversa en problemas de movimiento a velocidad constante ... ( Artículo escrito en catalán )

[nota del autor]

Fracciones generatrices ...

Proporcionalidad ...

Algunas nociones importantes: Una raó aritmètica és un quocient entre dos nombres reals obtinguts de les respectives mesures. Podem matisar una mica més aquesta definció: Una raó aritmètica entre dues quantitats, q1 i q1, és un nombre real que expressa la primera si prenem com a patró de mesura la segona: q1/q2. També és una raó aritmètica el quocient entre els valors de les mesures corresponents a dues magnituds M i N, m1/n1: m2/n2 ... Val a dir que s'anomena proporció a la igualtat entre dues raons aritmètiques, a/b i c/d: a/b = c/d. En una proporció es comleix que a.d = b.c La proporcionalitat com a tipus particular de relació de dependència entre magnituds Direm que una relació entre dues magnituds, M i N, és directa si un increment positiu en una comporta un increment positiu en l'altra. Una relació és inversa si un increment positiu d'una les dues comporta un increment negatiu en l'altra. Proporcionalitat directa entre dues magnituds M i N Donades dues magnituds M i N, direm que són magnituds directament proporcionals si per cada valor d'una d'elles mi es pot trobar un valor emparellat de l'altra, ni: {(m1,n1), (m2,n2), ...} de tal manera que m1/n1 = m2/n2 = m3/n = ... etcètera. Aquest valor constant s'anomena raó de proporcionalitat directa. Proporcionalitat inversa entre dues magnituds M i N Donades dues magnituds M i N, direm que són magnituds inversament proporcionals si per cada valor d'una d'elles mi es pot trobar un valor emparellat de l'altra, ni: {(m1,n1), (m2,n2), ...} de tal manera que m1/(1/n1) = m2/(1/n2) = m3/(1/n) = ... etcètera. Aquest valor constant s'anomena raó de proporcionalitat inversa.

Problemas de movimiento a velocidad constante

Problema 1 Jaume i Magda, que es troben a 7 km l'un de l'altra, caminen en sentits oposats per un sender de muntanya a un ritme força constant: Josep a una velocitat constant de 2 km/h; i Marta, a una velocitat constant de 3 km/h. Si surten a la mateixa hora, quant de temps passarà fins que es trobin ? A quina distància del punt de sortida de Josep es troben ? Resolució Sovint hom recorre a l'àlgebra per calcular una cosa com aquesta. De fet, no cal pas; n'hi ha prou a fer servir una senzilla proporció, cosa que permet trobar la solució fent càlcul mental. Vegem tot seguit com es pot fer. Com que en 1 h, la distància conjunta que recorren és de 5 km (comentari: aquesta velocitat de 5 km/h la podem entendre com la velocitat relativa: com si un dels dos es trobés en el punt de trobada, parat, i l'altre es mogués vers ell a aquesta velocitat), el temps t que cal per recorre una distància conjunta de 7 km surt de la proporció directa: t/7 = 1/5 D'aquí, t = 7/5 h = 1,4 h = 1 h i 12 min Per contestar la segona pregunta, el raonament aritmètic és encara més senzill: com que mantenint la velocitat, Josep recorre 2 km en 1 hora, en 7/5 h recorrerà 2.(7/5) = 14/5 km = 2,8 km = 2 km i 800 m desdel punt que ha començat a caminar Problema 2 Jaume i Magda, corren una marató. Com que estan ben entrenats, mantenen prou bé la velocitat: De mitjana, Jaume pot assolir un ritme de 4 minuts per quilòmetre, i Magda, necessita 5 minuts per recorre aquesta distància. Jaume ha arribat tard a la sortida: calcula que quan surt, Magda es troba a 1 quilòmetre de distància. Havien decidit anar junts fins a l'arribada. Quan de temps necessita Jaume per donar-li abast ? A quina distància de la sortida començaran a córrer junts ? Resolució Segons les dades de l'enunciat, Magda corre a una velocitat constant de 1/5 Km/min quan Jaume pren la sortida, a la màxima velocitat que pot assolir per tal de donar-li abast, 1/5 km/min. Fem, ara, la següent consideració per pensar la solució del problema d'una forma equivalent més senzilla, de tal manera que Jaume pugui calcular mentre corre (tingueu en compte que quan es fa exercici físic ens costa calcular): la situació equival a que Jaume corri a una velocitat relativa de 1/4 -1/5 = 1/20 km/min, i Magada estigui aturada a 1 km de distància. Vist així, és molt senzill: a Jaume li calen 20 minutos per recorrer aquest quilòmetre. Aquest és el temps que necessitarà per donar-li abast. La distància a què es troben del punt de sortida quan això succeeix és de: 20 min x 1/4 km/min = 5 km. Per cert, els queden 35 km i 195 m per correr junts ! (la distància que es corre en una marató és de 42 km i 195 m).

Relaciones útiles para calcular el volumen de un tronco de cono y el volumen de un tronco de pirámide

El problema de calcular el volumen de un tronco - pongamos que el de un cono, o el de una pirámide - se resuelve restando el volumen de la parte del cuerpo que truncamos del volumen del cuerpo completo.

TRONCO DE CONO
Así, al calcular el volumen de un tronco de cono, $V_{t.c.}$, conocido el valor del radio de cada una de las dos bases ( el mayor, $r_1$; y el menor, $r_2$ ) y la distancia entre ellas ( que denotamos por $d$ ), hemos deducido en clase tres relaciones que convendría apuntarlas en el formulario de ayuda para los exámenes:
(1) Denotando por $h_1$ la altura del cono completo, y por $h_2$ la del cono que truncamos, se cumple que $h_2+d=h_1$
(2) Cortando el cono por un plano axial, y empleando el Teorema de Tales, hemos visto que $\dfrac{h_1}{h_2}=\dfrac{r_1}{r_2}$
(3) Y, desde luego, $V_{t.c.}=\dfrac{1}{3}\,\pi\,r_{1}^{2}\,h_1-\dfrac{1}{3}\,\pi\,r_{2}^{2}\,h_2$

TRONCO DE PIRÁMIDE DE BASE CUADRADA
Por otra parte, al calcular el volumen de un tronco de pirámide, de base un cuadrado, $V_{t.p.b.c.}$, conocido el valor del lado de cada una de las dos bases ( el mayor, $l_1$; y el menor, $l_2$ ) y la distancia entre ellas ( que denotamos por $d$ ), también hemos deducido en clase tres relaciones que conviene apuntarlas en el formulario de ayuda para los exámenes:
(1) Denotando por $h_1$ la altura de la pirámide completa, y por $h_2$ la de la pirámide que truncamos, se cumple que $h_2+d=h_1$
(2) Cortando el cono por un plano axial que pose por los centros de ambas bases, y empleando el Teorema de Tales, hemos visto que $\dfrac{h_1}{h_2}=\dfrac{l_1}{l_2}$
(3) Y, desde luego, $V_{t.p.b.c.}=\dfrac{1}{3}\,l_{1}^{2}\,h_1-\dfrac{1}{3}\,l_{2}^{2}\,h_2$

[nota del autor]

Impuestos y descuentos. Calculando el valor nominal

ENUNCIAT
Hem comprat un article pel qual hem pagat 42 €. Aquesta quantitat ja porta incorporat l'IVA del 18% i també un descompte del 5% que ens han fet sobre el preu nominal de l'article. Quin és el valor d'aquest preu ?

SOLUCIÓ
Cal deduir l'IVA i deduir el descompte (l'ordre d'aquests dos passos no és rellevant). Calculem, primer, quant hauríem pagat (x) sense l'IVA del 18%; per això, cal plantejar la següent proporció:
$\dfrac{118}{100} = \dfrac{42}{x}$. D'aquí trobem que $x = \dfrac{2100}{59}$. A continuació, i a partir d'aquest resultat parcial, calculem quant ens hauria costat (el que acabem de trobar) si no ens haguessin fet el descompte (y): $\dfrac{95}{100}=\dfrac{\dfrac{2100}{59}}{y}$. I resolent la proporció trobem el preu nominal (sense descompte i sense IVA) de l'article $y \approx 37,47$ €
$\square$

Problemas de movimiento

Enunciat Josep i Marta, que es troben a 10 km l'un de l'altra, caminen en sentits oposats per trobar-se: Josep a una velocitat de 2 km/h, i Marta 3 km/h. Rosa, la filla de Marta, que va en bicicleta a una velocitat de 8 km/h, es dedica a anar de l'una a l'altre, sense parar, amunt i avall. Quina distància haurà recorregut la noia fins el moment que es trobin ? Resolució 1 En 1 h, la distància que recorren entre tots dos és de 5 km; Josep en fa dos vers Marta, i Marta tres vers Josep. Com que per fer una distància conjunta de 5 Km els cal 1 h, per fer 10 km els en calen 2 h. Llavors, després de 2 h de començar a caminar, quan es trobin, Josep haurà recorregut 4 km i Marta 6 km. Durant aquestes dues hores, Rosa no ha parat de moure's amunt i avall amb la seva bicicleta, recorrent 8 km cada hora, per tant durant aquestes dues hores de caminada fins que es troben Josep i Marta, Rosa haurà recorregut 16 km. Resolució 2 Observeu que el raonament basat en considerar la distància conjunta que s'ha recorregut en un hora - la que l'un ha fet en un sentit més la recorreguda en l'oposat per l'altre - no és més que la velocitat relativa: 5 km/h. El problema es resol per tant d'una forma molt simple en termes de velocitat relativa la qual cosa és equivalent a plantejar el problema com si un dels dos estigués posat en el punt de trobada, en repós, i l'altre s'acostés a una velocitat igual a al reltaiva. Per tant, si per fer cinc quilòmetres cal 1 hora, per fer-ne 10 en calen dues, que és el temps que tarda la persona que es mou (en el plantejament de moviment relatiu) a arribar al punt de trobada on l'espera la persona en repós (segons el plantejament equivalent del moviment relatiu). El pas final és el mateix: Rosa haurà recorregut durant aquestes dues hores, 8 k/m . 2 h = 16 km Resolució 3 Si x és la distància al punt de trobada, mesurada des del punt de sortida de Josep, 10 - x és la distància mesurada des del punt de sortida de Marta. Com que s'han de trobar en el temps, x/2 = (10-x)/3, equació de 1r grau que té com a solució x = 4 km (del punt de partida de Josep). Això correspon a un temps de 4/2 = (10-4)/3 = 2 h de caminada fins a trobar-se. Per tant, en aquestes dues hores, Rosa - a 8 km/h - haurà fet 16 km de distància anant de l'un a l'altra sense parar i fins que Josep i Marta es troben.

Clasificación de los sitemas de ecuaciones lineales

Un sistema d'igualtats algèbriques pot ser d'un dels tres tipus següents: SISTEMA COMPATIBLE DETERMINAT. A cada incògnita li correspon un únic valor. Les equacions són independents: cada una aporta una informació diferent a les altres, la qual cosa permet determinar un únic valor per a cada incògnita. Exemple (sistema compatible determinat de dues equacions amb dues incògnites) x+y=1 x-y=2 SISTEMA COMPATIBLE INDETERMINAT. A cada incògnita li correspon infinits valors com a solució ja que algunes de les equacions són equivalents a d'altres i, per tant, no el conjunt d'equacions no aporta informació suficient per poder determinar valors únics per a cada incògnita. Exemple (sistema compatible indeterminat de dues equacions amb dues incògnites) x+y=1 2x+2y=2 SISTEMA INCOMPATIBLE. No es pot trobar cap solució (no n'hi ha, de fet) perquè les equacions són contradictòries Exemple (sistema incompatible de dues equacions amb dues incògnites) x+y=1 x+y=2

Los diversos tipos de igualdades algebraicas

Una igualtat algèbrica (equació) es pot ser d'un dels tres tipus següents: EQUACIÓ COMPATIBLE DETERMINADA. A cada incògnita li correspon un únic valor. Exemple (amb una sola incògnita): x+1=2 EQUACIÓ COMPATIBLE INDETERMINADA o IDENTITAT. A cada incògnita li correspon infinits valors com a solució degut al fet que els dos membres de la igualtat donen la mateixa informació però expressada de forma diferent, amb la qual cosa no podem determinar un únic valor per a la incònita. Exemple (amb una sola incògnita): 2(x+1) = 2x+2 EQUACIÓ INCOMPATIBLE. No té solució perquè els membres de la igualtat donen informació contradictòria Exemple (amb una sola incògnita): x=x+1

Políedros regulares

PASADO A LOS BLOGS

A l'escrit anterior parlava del teorema d'Euler, vàlid per als poliedres convexos, que són els que no tenen entrades. Tenim un eina valuosa per investigar les relacions dels poliedres: un graf planar que anomenem diagrama d'Schlegel. Tot poliedre convex el podem representar per un graf planar, resultat d'imaginar el poliedre col·lapsat sobre un pla, fent distinció de totes les seves arestes i vèrtexs. Doncs bé, un graf planar compleix que v-a+c=1 (on, ara, v representa un punt on hi van a parar vàries arestes i, per cara, entenem l'espai de pla tancat per dues arestes les quals no cal que les dibuixem pas rectilínies. De fet, si comptem la cara exterior com una cara més, podem expressar-lo talment com el teorema d'Euler, v-a+c=2. La figura mostra els grafs corresponents al tetraedre (v=4, a=6, c=3) i a l'ocatedre (c=8, v=9, a = 16). Observem que, efectivament, es compleix el resultat que comento: 4-6+3=1, i 9-16+8=1), de la mateixa manera que es compleix en tots els grafs planars Tot això té interessants aplicacions, com ara el disseny i anàlisi de circuïts elèctrics, anàlisi de l'estructura molecular.

Los lados de un triángulo rectángulo miden

Enunciat:
Els costats d'un triangle rectangle mesuren $6 \; \text{cm}$, $8 \; \text{cm}$, i $10 \; \text{cm}$. Us demanem:
    a) Un dibuix esquemàtic del triangle, posant les lletres convenients (respecteu el conveni) als vèrtexs, als costats, i als angles
    b) Construïu, amb regle i compàs, el triangle (a escala, si cal)
    c) Calculeu l'àrea del triangle
    d) Calculeu el perímetre del triangle

Resolució:
  a)

$\square$

  b)
Adoneu-vos que es tracta d'un triangle rectangle; per això, tan sols cal que observeu que les longituds dels costats $\{6,8,10\}$ formen una terna pitagòrica, o bé, feu un cop d'ull a la figura que hem dibuixat a l'apartat anterior: l'angle que formen els dos costats més curts és un angle recte.

Llavors, l'àrea serà igual a
$\mathcal{A}=\dfrac{6 \cdot 8}{2}=24 \, \text{cm}^2$

$\square$

  b)
El perímetre (suma de les longituds dels tres costats) és igual a
$\mathcal{P}=24 \, \text{cm}$
$\square$

El $5\%$ de una cierta cantidad de bolas es

Enunciat:
El $5\%$ d'una determinada quantitat de boles és igual a $3$ boles. Quantes boles representen el $90\%$ del total de boles ? [Instrucció: Resoleu el problema sense calcular, prèviament, el nombre total de boles (exercici de destresa algèbrica)].

Solució:

Anomenem:
    $x$, al nombre total de boles
    $y$, al nombre de boles que correspon al $90\%$ de $x$

Plantegem les següents proporcions:

    $\dfrac{5}{100}=\dfrac{3}{x} \quad \quad \quad (1)$


    $\dfrac{90}{100}=\dfrac{y}{x} \quad \quad \quad (2)$

Dividint, membre a membre, la igualtat (2) entre la igualtat (1), s'obté

    $\dfrac{90}{100} \div \dfrac{5}{100}=\dfrac{y}{x}\div \dfrac{3}{x}$

fent les divisions i simplificant, queda

    $\dfrac{90}{5}=\dfrac{y}{3}$

i, d'aquí, s'ha de complir que

    $90 \cdot 3 = 5 \, y$

llavors,

    $y=\dfrac{90 \cdot 3}{5}$

        $=54$   boles

$\square$

Una persona ha ido a comer a un restaurante

Enunciat:
Una persona ha anat a dinar a un restaurant. Li ha costat $9,50 \; \text{euros}$   ( amb un IVA del $10 \,\%$ inclòs sobre el preu del dinar ). Si aquest impost no fos de tipus reduït (del $10\%$, aplicat als restaurants i a l'hostatgeria ), ans fos del tipus habitual per al comerç ( $21\%$ ), quant li hauria costat el dinar ?

Solució:

Anomenem:
    $x$, al preu del dinar ( sense el càrrec de l'impost del $10\%$ )
    $y$, a la quantitat a pagar ( amb el càrrec de l'impost del $21\%$ sobre $x$ )

Plantegem les següents proporcions:

    $\dfrac{100}{100+110}=\dfrac{x}{9,50} \quad \quad \quad (1)$


    $\dfrac{100+21}{100}=\dfrac{y}{x} \quad \quad \quad (2)$

Multiplicant, membre a membre, les igualtats (2) i (1), s'obté

    $\dfrac{121}{100}\cdot \dfrac{100}{110}=\dfrac{y}{x}\cdot \dfrac{x}{9,50}$

expressió que, simplificant $x$, queda

    $\dfrac{121}{110}=\dfrac{y}{9,50}$

i, d'aquí, s'ha de complir que

    $121 \cdot 9,50 = 110 \, y$

llavors,

    $y=9,50 \cdot \dfrac{121}{110}$

        $=10,45 \; \text{euros}$

$\square$

Los vecinos de una comunidad ...

ENUNCIADO:
Los vecinos de una comunidad se han reunido para decidir si contratan o no un determinado servicio. Después de debatir los pros y los contras se ha realizado una votación, y el resultado de la misma ha sido el siguiente: las tres cuartas partes se han manifestado a favor; la mitad de los restantes, en contra; y ocho vecinos se han abstenido. ¿ Cuántos vecinos hay en la comunidad ?.

SOLUCIÓN:
La parte del vecindario que vota o bien sí o bien no es $\dfrac{3}{4}+\dfrac{1}{2}\,\left(1-\dfrac{3}{4}\right)$, que es igual a $\dfrac{7}{8}$; así, pues, la parte del vecindario que se abstiene es igual a $1-\dfrac{7}{8}=\dfrac{1}{8}$; con lo cual, denotando por $x$ el número de vecinos, podemos plantear la siguiente proporción $$\dfrac{1}{8}=\dfrac{8}{x}$$
de donde, despejando la incógnita,
$$x=8 \cdot 8 = 64 \, \text{vecinos}$$
$\square$

Otra demostración del Teorema de Pitágoras

Teorema de Pitàgores:
Com és ben sabut, donat el triangle rectangle de vèrtexs A, B i C, es compleix la següent propietat entre les longituds dels seus costats ( la hipotenusa $b$, i els dos catets $a$ i $c$ )
                                                    $b^2=a^2+c^2$

Una demostració més (en aquest blog n'he exposat ja unes quantes) d'aquest teorema (n'hi ha més d'un centenar) és la següent.

Demostració:
Si repliquem el triangle rectangle tal com es mostra a la figura, és ben fàcil veure que, donada la disposició de les parts, l'àrea del quadrat gran $(a+c)^2$ es pot calcular de dues maneres:
        i) Desenvolupant el binomi al quadrat, podem escriure
          $(a+c)^2 = a^2+2\,a\,c+c^2 \quad \quad (1)$
        ii) Tenint en compte que l'àrea del quadrat gran es descompon en quatre triangles rectangles ( de costats $a$ i $c$ ) i el quadrat del centre de la figura ( de costat $b$ ), podrem expressar la seva àrea com la suma
          $(a+c)^2 = b^2 + 4\cdot \dfrac{a\,c}{2} \quad \quad \quad (2)$
Igualant, ara, els segons membres de (1) i (2)
    $a^2+2\,a\,c+c^2=b^2 + 4\cdot \dfrac{a\,c}{2}$
i simplificant
    $a^2+2\,a\,c+c^2=b^2 + 2 \, a\,c$
    $b^2=a^2+2\,a\,c-2 \, a\,c+c^2$
arribem a la igualtat que volíem demostrar
    $b^2=a^2+c^2$
$\square$

El $5\%$ de una cierta cantidad de bolas

Enunciat:
El $5\%$ d'una determinada quantitat de boles és igual a $3$ boles. Quantes boles representen el $90\%$ del total de boles ?.

Solució:

Anomenem:
    $x$, al nombre total de boles

Calculem, primer de tot, el nombre total de boles plantejant la següent proporció:

    $\dfrac{5}{100}=\dfrac{3}{x}$

d'aquí, s'ha de complir que

    $5\, x = 100 \cdot 3$

llavors, el nombre total de boles és

    $x=\dfrac{100 \cdot 3}{5}$

        $=60$   boles

Calculem, ara, quant representa el $90\%$ d'aquestes $60$ boles (anomenem a $y$ a aquesta quantitat); per això plantegem la proporció,

    $\dfrac{90}{100}=\dfrac{y}{60}$

d'aquí s'ha de complir que

    $90 \cdot 60 =100 \, y$

llavors

    $y=\dfrac{90\cdot 60}{100}$

      $=\dfrac{5400}{100}$

      $=54$ boles

$\square$

Operar con fracciones

ENUNCIADO:
Efectuar las siguientes operaciones con fracciones:
a) $\dfrac{2}{3}-\dfrac{5}{6}+\dfrac{1}{2}$

b) $\dfrac{4}{9}\cdot \dfrac{3}{2}$

c) $\dfrac{6}{12}\div \dfrac{3}{4}$

d) $\dfrac{1}{2} \cdot \dfrac{4}{3}-\dfrac{1}{3}$

SOLUCIÓN:

a)
$\dfrac{2}{3}-\dfrac{5}{6}+\dfrac{1}{2}=$

    $=\dfrac{4}{6}-\dfrac{5}{6}+\dfrac{3}{6}$ ( reduciendo a común denominador )

    $=\dfrac{4-5+3}{6}$ ( operando los numeradores )

    $=\dfrac{2}{6}$ ( simplificando ...)

    $=\dfrac{1}{3}$

b)

$\dfrac{4}{9}\cdot \dfrac{3}{2}=\dfrac{4 \cdot 3}{9 \cdot 2} = \dfrac{4 \cdot 3}{2 \cdot 9}=\dfrac{2 \cdot 1}{1 \cdot 3}=\dfrac{2}{3}$

c)

$\dfrac{6}{12}\div \dfrac{3}{4}=\dfrac{1}{2}\div \dfrac{3}{4}=\dfrac{1}{2}\cdot \text{inv}\left( \dfrac{3}{4}\right)=\dfrac{1}{2}\cdot \dfrac{4}{3} = \dfrac{1 \cdot 4}{2 \cdot 3}= \dfrac{4 \cdot 1}{2 \cdot 3} = \dfrac{2 \cdot 1}{1 \cdot 3} =\dfrac{2}{3}$

d)

$\dfrac{1}{2} \cdot \dfrac{4}{3}-\dfrac{1}{3}=\dfrac{1 \cdot 4 }{2 \cdot 3} - \dfrac{1}{3}=\dfrac{4 \cdot 1}{2 \cdot 3} - \dfrac{1}{3}=\dfrac{2 \cdot 1}{1 \cdot 3} - \dfrac{1}{3}=\dfrac{2}{3}-\dfrac{1}{3}=\dfrac{1}{3}$

$\square$

Construcción de polígonos irregulares con regla y compás

Enunciado:
A partir de cuatro segmentos de longitud dada ( parte superior de la figura ), construir con ellos ( empleando la regla y el compás ) un polígono.

Solución:

$\square$

Cálculo con potencias

Enunciado:
Expresar como una potencia única:
    $4^3\cdot 2^5 \div 8$

Solución:
Teniendo en cuenta que $4=2^2$
y que $8=2^3$, podemos escribir
    $4^3\cdot 2^5 \div 8$
de la forma
      $\big(2^2\big)^3\cdot 2^5 \div 2^3$
      $=2^{2 \cdot 3} \cdot 2^5 \div 2^3$
      $=2^{6} \cdot 2^5 \div 2^3$
      $=2^{6+5-3}$
      $=2^{8}$
$\square$

[nota del autor]

Averiguar si el número $36$ es un n. triangular. ( Artículo escrito en catalán )

Enunciat:
Esbrineu si el nombre natural $36$ és triangular.

Solució:
Si és un n. triangular ha d'existir un nombre $n \in \mathbb{N}$, més petit que $36$, tal que
                $\dfrac{n\,(n+1)}{2}=36$
Cal, per tant, resoldre aquesta equació; si algun dels valors de la solució és un nombre natural més petit que $36$. Vegem-ho:
Podem escriure l'equació de la forma
                $n^2+n-72=0$
que és una equació polinòmica de 2n grau completa. Resolent-la, obtenim dos valors com a solució: $-9$ ( que, en ser un nombre enter negatiu, no ens interessa ) i $8$, que sí satisfà la condició i, per tant, queda demostrat que $36$ és un nombre triangular.
$\square$

Usos de la calculadora científica

Enunciat:
Feu servir la calculadora científica bàsica per determinar el valor del quocient i del residu de la divisió entera $112\,563 \div (-259)$

Solució:
La calculadora científica bàsica no disposa de la funció MOD per calcular el valor del residu; com a recurs, podem efectuar la divisió decimal, obtenint el següent valor $-434,\overline{6061777}$, amb la qual cosa, podem afirmar que, éssent no nul·la la part decimal del quocient (de la divisió decimal), el residu del la divisió entera és diferent de zero. Llavors, si $D$ és el dividend, $d$ el divisor, $q$ el quocient, i $r$ el residu, pel teorema de la visió euclidiana, s'haurà de complir
    $D=d\cdot q+r \quad \text{on} \quad 0 \le r \prec \left|d\right|$

Efectuant la divisió:
      $q=-434$, ja que $-434 \cdot (-259) = 112\,406 \prec 112\,563$
      i, a partir d'aquest resultat, calculem el valor del residu:
      $r=112\,563-112\,406$
        $ = 157$

$\square$

Resolución de una ecuación de segundo grado completa, transformándola convenientemente

Enunciat:
Resoleu l'equació $x^2+x-1=0$ sense fer ús de l'expressió general de la solució d'una equació de 2n grau completa.

Solució:
Fent ús de la identitat notable $(m+n)^2=m^2+2\,m\,n+n^2$, podem escriure el primer membre de la següent forma
  $\bigg(x+\dfrac{1}{2}\bigg)^2-\bigg(\dfrac{1}{2}\bigg)^2-1$
que, simplificat, queda
  $\bigg(x+\dfrac{1}{2}\bigg)^2-\dfrac{5}{4}$
per tant l'equació original, escrita d'una manera més convenient per poder trobar la solució, és equivalent a la següent
  $\bigg(x+\dfrac{1}{2}\bigg)^2-\dfrac{5}{4}=0$
llavors
  $\bigg(x+\dfrac{1}{2}\bigg)^2=\dfrac{5}{4}$
i extraient l'arrel quadrada a cada membre de la igualtat per desfer la potència al quadrat del primer membre obtenim
  $\pm \left(x+\dfrac{1}{2}\right)=\sqrt{\dfrac{5}{4}}$
  $ x+\dfrac{1}{2}=\pm\,\sqrt{\dfrac{5}{4}}$
per tant,
  $x=-\dfrac{1}{2}\pm \dfrac{\sqrt{5}}{2}$
        $=\dfrac{-1\pm \sqrt{5}}{2}$
és a dir
$x=\left\{\begin{matrix}\dfrac{-1 + \sqrt{5}}{2}\\\vee\\\dfrac{-1 -\sqrt{5}}{2} \\ \end{matrix}\right.$
$\square$

Calcular el mínimo común múltiplo y el máximo común divisor de los números enteros ... ( Artículo escrito en catalán )

Enunciat:
    Calculeu
      a) el màxim comú divisor de $-72$ i $-84$
      b) el mínim comú múltiple de $-72$ i $-84$

Solució:
  a)
Tinguem en compte que, tractant amb nombres enters que, en aquest cas, son negatius:
    $\text{m.c.d}(-72,-84)=\text{m.c.d}(\left|-72\right|,\left|-84\right|)$
Factoritzant ambdós nombres obtenim
      $72=2^3\cdot 3^2$
      $84=2^2\cdot 3 \cdot 7$
per tant
    $\text{m.c.d}(-72,-84)=\text{m.c.d}(\left|-72\right|,\left|-84\right|)=\pm ( 2^2\cdot 3 ) = \pm 12$

  b)
Emprant la propietat
        $\text{m.c.m}(a,b) \times \text{m.c.d}(a,b)=a \cdot b$
obtenim
        $\text{m.c.m}(-72,-84) = \big((-72)\cdot (-84)\big) \div \text{m.c.d}(-72,-84)$
                                        $= \big((-72)\cdot (-84)\big) \div ( \pm 12 )$
                                        $= 6\,048 \div ( \pm 12 )$
                                        $= \pm 504$

$\square$

[nota del autor]

Un grupo de jóvenes asisten a una fiesta. Si se marchasen tres chicos

Enunciat:
Quaranta-tres joves assisteixen a una festa. Si marxessin 3 nois, hi hauria el triple de noies que de nois. Quantes noies hi havia?

Solució:
Designem amb $n$ el nombre de nois que inicialment hi ha a la festa; llavors, si en marxen tres, $n-3$ és el nombre de nois que es queden.

Tenint en compte, a més a més, que en marxar tres persones hi quedaran 40 persones i que el nombre de noies (en aquesta situació) [ que és $40-(n-3)$ ] ha de ser el triple que el de nois, escriurem la següent equació,

              $40-(n-3)=3\,(n-3)$

Resolent aquesta equació trobarem el nombre de nois que hi havia inicialment a la festa:

        $40-(n-3)=3\,(n-3)$
        $40=4\,(n-3)$
        $10=n-3$
        $n=10+3$
          $=13 \quad \text{nois}$

Per tant hi queden $13-3=10 \quad \text{nois}$ i $3\cdot 10= 30 \quad \text{noies}$. I com que no ha marxat cap noia, a la festa hi havia inicialment $30$ noies ( i $1 3$ nois).

$\square$

La suma de dos números naturales consecutivos es ...

Enunciat:
La suma de dos nombres naturals senars consecutius és igual a 156. Determineu aquests nombres.

Solució:
Si $n$ és un nombre enter positiu ( $ n=0,1,2,\ldots $ ), llavors $2\,n+1$ és un nombre senar, i $(2\,n+1)+2$ és el nombre senar consecutiu al primer. D'acord amb la informació de l'enunciat podrem plantejar la següent equació:
              $(2\,n+1)+\big((2\,n+1)+2\big)=156$
Resolem-la:
      $(2\,n+1)+\big((2\,n+1)+2\big)=156$
        $2\,n+1+2\,n+3=156$
        $4\,n+4=156$
        $4\,n=156-4$
        $n=\dfrac{152}{4}$
              $=38$
D'aquest valor de $n$ trobem, doncs, els valors del primer nombre senar demanat
        $2\,n+1=2 \cdot 38+1$
          $=77$
i del seu senar consecutiu
        $2\,n+3=2 \cdot 38+3$
          $=77+2$
          $=79$
$\square$

Queremos embaldosar el suelo de una habitación rectangular con baldosas cuadradas ...

Enunciat:
    Volem enrajolar una habitació rectangular amb el nombre més petit possible de rajoles quadrades, sense haver de trencar i ajustar les rajoles. Els costats de l'habitació mesuren $420 \; \text{cm}$ i $528 \; \text{cm}$, respectivament. De quina mida han de ser les rajoles ? Quantes rajoles necessitarem ?

Solució:
    Imaginant una fila de rajoles al llarg d'un dels costats veiem que n'hi ha d'haver un nombre enter (no ha de faltar ni sobrar cap tros de rajola); i, al llarg de l'altre costat ha de passar el mateix. Llavors, el costat $c$ de les rajoles ha de correspondre al màxim comú divisor de les longituds dels costats de l'habitació:
                                      $c=\text{m.c.d.(420,528)}=12 \; \text{cm}$
Llavors, el nombre de rajoles és igual al nombre de quadrats amb què podem quadricular l'habitació rectangular; necessitem, per tant, el següent nombre de rajoles
                                      $\dfrac{420}{12}\cdot \dfrac{528}{12}=35 \cdot 44 = 1\,540 \, \text{rajoles}$
$\square$

María tiene cuatro mandarinas menos que Sara ...

Enunciat:
La Maria té 4 mandarines menys que la Sara. Si la Maria li'n donés dues, la Sara en tindria el triple que ella. Quantes mandarines té cadascuna ?

Solució:
Anomenem $s$ al nombre de mandarines que té la Sara abans que en doni dues a la Maria.

Llavors, podem plantejar l'equació que expressa, en el llenguatge de l'àlgebra, la informació de l'enunciat. Tenint en compte el nombre inicial de mandarines que tenia cada una i la transferència de mandarines que es descriu, podrem escriure:

          $3\,\big((s-4)-2 \big)=s+2$

  On, al primer membre, i, dins del primer parèntesi, $s-4$ representa el nombre de mandarines que té la Maria (abans que la Sara li'n doni dues de les seves); i, al segon membre, $s+2$ és el nombre de mandarines que tindrà la Sara quan la Maria li'n doni dues de les seves. El factor $3$ que hi ha davant del primer parèntesi del primer membre indica que el nombre de mandarines amb què es quedarà la Maria serà igual a una tercera part de les que arribarà a tenir la Sara, és a dir, la Sara en tindrà el triple de les que tindrà la Maria.

Resolem, ara, l'equació:
      $3\,\big((s-4)-2 \big)=s+2$
        $3\,(s-6 )=s+2$
        $3\,s-18=s+2$
        $3\,s-s=2+18$
        $2\,s=20$
        $s=10$, que és el nombre de mandarines que té la Sara (abans que en doni dues d'aquestes a la Maria).

I, d'aquí, deduïm que la Maria té $10-4=6$ mandarines ( abans de fer la transferència).

$\square$

En una caja hay bolas blancas y negras ...

Enunciat:
En una capsa hi ha boles blanques i negres. La diferència entre el nombre de boles blanques i el nombre de boles negres és 1. Si retirem 3 boles negres de la capsa, el nombre de boles blanques que hi haurà, ara, dins de la capsa serà el triple que el nombre de boles negres que hi quedaran.
    a Quantes boles blanques hi ha inicialment a la capsa?
    b) Quantes boles hi ha inicialment a la capsa?

Solució:
  a)
Anomenem amb $b$ el nombre de boles blanques que, inicialment, hi ha a la capsa.

D'acord amb la informació de l'enunciat sabem que:
    $b-1$ és el nombre inicial de boles negres que hi ha a la capsa
    $(b-1)-3$ és el nombre final de boles negres que hi quedaran a la capsa
    $3\big((b-1)-3\big)$ és el nombre final de boles blanques que hi quedaran a la capsa. Llavors,
          $3\big((b-1)-3\big)=b$
            $3\,(b-4)=b$
            $3\,b-12=b$
            $3\,b-b=12$
            $2\,b=12$
            $b=6 \quad \text{boles blanques}$

  b)
El nombre de boles negres que hi ha (inicialment) a la capsa és igual a $(b-1)|_{b=6}=6-1=5 \quad \text{boles negres}$. Per tant, el nombre de boles que, inicialment, hi ha a la capsa és $6+5=11$ boles en total.

$\square$

Ecuaciones de primer grado con coeficientes fraccionarios ...

Resoleu l'equció:
    $\dfrac{2}{15}\,x+\dfrac{1}{12}=\dfrac{7}{75}-\dfrac{5}{36}\,x$

Solució:
  Procediment A:
Observem que es tracta d'una equació de primer grau amb una incògnita i amb coeficients fraccionaris. Multiplicant ambdós membres de la igualtat pel mínim comú múltiple del conjunt de denominadors dels coeficients, i, simplificant, obtindrem una equació equivalent amb coeficients enters, que serà més senzilla.

Calculem el mínim comú múltiple dels denominadors de dels coeficients
    $\{\dfrac{2}{15}\,,\,\dfrac{1}{12}\,\,,\,\dfrac{7}{75}\,,\,\dfrac{5}{36}\}$
i obtenim
$\text{m.c.m}(15,12,75,36)=3^2\cdot 5^2 \cdot 2^2 = 900$
Multiplicant els dos membres de l'equació per aquest nombre podrem escriure l'equació equivalent
    $900\cdot \dfrac{2}{15}\,x+900\cdot \dfrac{1}{12}=900\cdot \dfrac{7}{75}-900\cdot \dfrac{5}{36}\,x$
que, simplificant, queda
    $120\,x+75=84-125\,x$
Agrupant, ara, els termes semblants a un i altre membre de la igualtat arribem a
    $120\,x+125\,x=84-75$
i, operant, s'obté
    $245\,x=9$
d'on, aïllant la incògnita s'arriba al valor d'aquesta que satisfà al igualtat plantejada
    $x=\dfrac{9}{245}$
$\square$

  Variant del procediment A:
Reduïm a comú denominador els coeficients fraccionaris:
    $\{\dfrac{2}{15}\,,\,\dfrac{1}{12}\,\,,\,\dfrac{7}{75}\,,\,\dfrac{5}{36}\}$
obtenint el conjunt de fraccions de denominador comú
    $\{\dfrac{2 \cdot (900 \div 15)}{900}\,,\,\dfrac{1 \cdot (900 \div 12)}{900}\,\,,\,\dfrac{7 \cdot (900 \div 75)}{900}\,,\,\dfrac{5 \cdot (900 \div 36)}{900}\}$
que, fent les operacions, són
    $\{\dfrac{120}{900}\,,\,\dfrac{75)}{900}\,\,,\,\dfrac{84}{900}\,,\,\dfrac{125}{900}\}$
En substituir els coeficients originals pels corresponents equivalents que acabem de calcular podrem escriure l'equació original de la forma
    $\dfrac{120}{900}\,x+\dfrac{75}{900}=\dfrac{84}{900}-\dfrac{125}{900}\,x$
és a dir
    $\dfrac{120\,x+75}{900}=\dfrac{84-125\,x}{900}$
i multiplicant per $900$ a cada membre
    $900\ cdot \dfrac{120\,x+75}{900}=900\,\dfrac{84-125\,x}{900}$
podrem simplificar i escriure-la de la manera següent
    $120\,x+75=84-125\,x$
i, finalment, agrupant els termes semblants a cada costat de l'igual
    $120\,x+125\,x=84-75$
que, per la propietat distributiva de la multiplicació respecte de la suma, és equivalent a
    $(120+125)\,x=84-75$
operant s'obté
    $245\,x=9$
i, dividint ambdós membres per $245$
    $\dfrac{245\,x}{245}=\dfrac{9}{245}$
i simplificant, ens quedarà aïllada la incògnita
    $x=\dfrac{9}{245}$
$\square$

  Procediment B:
Operarem, ara, amb nombres fraccionaris i, per tant, agrupem ja els termes semblants a cada membre de la igualtat. A partir de l'equació original
    $\dfrac{2}{15}\,x+\dfrac{1}{12}=\dfrac{7}{75}-\dfrac{5}{36}\,x$
podem escriure
    $\dfrac{2}{15}\,x+\dfrac{5}{36}\,x=\dfrac{7}{75}-\dfrac{1}{12}$
i, per la propietat distributiva del producte respecte de la suma, ho podem posar així
    $\big(\dfrac{2}{15}+\dfrac{5}{36}\big)\,x=\big(\dfrac{7}{75}-\dfrac{1}{12}\big)$
a partir d'aquí, sumant els coeficients fraccionaris; s'obté
    $\dfrac{49}{180}\,x=\dfrac{1}{100}$
és a dir
    $\dfrac{49}{18}\,x=\dfrac{1}{10}$
i aïllant la incògnita arribem a
    $x=\dfrac{\frac{1}{10}}{\frac{49}{18}}$
i efectuant el quocient de les fraccions trobem
            $x=\dfrac{18}{490}$
resultat que, simplificat, queda
            $x=\dfrac{9}{245}$
$\square$

Nota 1: Per comprovar que el resultat és obtingut cal substituir-lo a l'equació original i mirar si les quantitats que s'obtenen a cada membre són iguals. Vegem-ho.
L'equació original és
    $\dfrac{2}{15}\,x+\dfrac{1}{12}=\dfrac{7}{75}-\dfrac{5}{36}\,x$
Substituint, trobem que el primer membre és igual a
    $\dfrac{2}{15}\cdot \dfrac{9}{245}+\dfrac{1}{12}$
que, operant, queda
            $\dfrac{1297}{14700}$
i que el segon membre té el següent valor
    $\dfrac{7}{75}-\dfrac{5}{36}\cdot \dfrac{9}{245}$
que també és igual a
            $\dfrac{1297}{14700}$
Per tant, queda comprovat el resultat obtingut.

Nota 2: En general, no és convenient operar amb les expressions decimals dels coeficients fraccionaris dels termes de l'equació, per vàries raons: a) les expressions decimal d'aquests coeficients fraccionaris són de tipus decimal periòdic:

  $\dfrac{2}{15}=0,1\bar{3}$
  $\dfrac{1}{12}=0,08\bar{3}$
  $\dfrac{7}{75}=0,09\bar{3}$
  $\dfrac{5}{36}=0,13\bar{8}$

Per tant, ens veuríem obligats a fer aproximacions; és a dir, no obtindríem el resultat exacte ans un d'aproximat la qual cosa, en aquest exercici és innecessari i, doncs, inacceptable; b) treballar amb expressions decimals és gairebé sempre més farragós i feixuc que fer ús del càlcul amb fraccions (que podem realitzar amb les funcions de càlcul fraccionari de la calculadora científica bàsica ).

Calcular la fracción resultante ...

Enunciat:
Efectueu la següent operació amb fraccions:
      $\big(\dfrac{5}{12}-\dfrac{7}{30}+\dfrac{1}{2}\div \dfrac{3}{4}\big)\cdot \dfrac{60}{5}$

Solució:
Primer de tot, simplifiquem les fraccions que siguin reductibles:
    $\dfrac{60}{5}=12$
i tornem a escriure l'expressió numèrica equivalent
      $\big(\dfrac{5}{12}-\dfrac{7}{30}+\dfrac{1}{2}\div \dfrac{3}{4}\big)\cdot 12$
A continuació, respectant la prioritat de les operacions, efectuem primer les que hi ha dins del parèntesi, per tant, efectuem en primer lloc la divisió
    $\dfrac{1}{2}\div \dfrac{3}{4}=\dfrac{1}{2}\cdot \text{inv}\big(\dfrac{3}{4}\big)=\dfrac{1}{2}\cdot \dfrac{4}{3}=\dfrac{1\cdot 4}{2 \cdot 3}=\dfrac{4}{2}\cdot \dfrac{1}{3}=2 \cdot \dfrac{1}{3}=\dfrac{2}{3}$
Posem aquest resultat a la línia principal del càlcul i continuem
      $\big(\dfrac{5}{12}-\dfrac{7}{30}+\dfrac{1}{2}\div \dfrac{3}{4}\big)\cdot 12$
        $=\big(\dfrac{5}{12}-\dfrac{7}{30}+\dfrac{2}{3}\big)\cdot 12$
A continuació, continuem fent les operacions del parèntesi, que són sumes i restes, per tant reduïm a comú denominador ( $ \text{m.c.m}(12,30,3)=60$ ) i trobem que
      $\dfrac{5}{12}-\dfrac{7}{30}+\dfrac{1}{2}$
        $=\dfrac{5 \cdot (60 \div 12)}{60}-\dfrac{7 \cdot (60 \div 30) }{30}+\dfrac{1 \cdot ( 60 \div 2)}{2}$
        $=\dfrac{25}{60}-\dfrac{14}{60}+\dfrac{40}{60}$
        $=\dfrac{25-14+40}{60}$
        $=\dfrac{51}{60}$
        $=\dfrac{17}{30}$
Posem aquest resultat a la línia principal del càlcul i continuem
      $\big(\dfrac{5}{12}-\dfrac{7}{30}+\dfrac{2}{3}\big)\cdot 12$
        $=\dfrac{17}{20}\cdot 12$
        $=17\cdot \dfrac{12}{20}$
        $=17\cdot \dfrac{3}{5}$
        $=\dfrac{51}{5}$
$\square$

Fracciones equivalentes

Enunciat:
Donats els nombres racionals equivalents $\frac{a}{b}$ i $\frac{c}{d}$, justifiqueu la següent propietat:
                $\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}$

Solució:
Si
$\dfrac{a}{b}=\dfrac{a+c}{b+d}$
llavors,
$a\,(b+d)=b\,(a+c)$
és a dir
$a\,b+a\,d=b\,a+b\,c$
i, donat que $a\,b=b\,a$
la igualt anterior és equivalent a
$a\,b+a\,d=a\,b+b\,c$
Sumant $-a\,b$ a cada membre queda
$-a\,b+a\,b+a\,d=-a\,b+a\,b+b\,c$
i simplificant,
$a\,d=b\,c$
Finalment, dividint ambdós membres de la igualtat per $b\,d$ ens queda
$\dfrac{a}{b}=\dfrac{c}{d}$
Hem acabat.

Exemple:
Si
$\dfrac{2}{3}=\dfrac{4}{6}$
llavors
$\dfrac{2}{3}=\dfrac{4}{6}=\dfrac{2+4}{3+6}$
        $=\dfrac{6}{9}$

Comentari:
També es compleix que
$\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a-c}{b-d}=\dfrac{c-a}{d-b}$

Exemple:
$\dfrac{24}{15}=\dfrac{8}{5}=\dfrac{16}{10}=\dfrac{-16}{-10}$

Observació:
Atenció, però. Tingueu en compte que a partir de
      $\dfrac{a}{b}=\dfrac{c}{d}$
no es pot caure en la temptació d'escriure coses errònies; per exemple, cal tenir en compte que
      $\dfrac{a}{b}=\dfrac{c}{d} \neq \dfrac{a\,c}{b\,d}$

Exemple:
$\dfrac{2}{3}=\dfrac{4}{6} \neq \dfrac{2 \cdot 4}{3 \cdot 6}$

$\square$

El perímetro de un triángulo rectángulo ...

Enunciat:
El perímetre d'un triangle rectangle mesura vint-i-quatre metres, i, la longitud d'un dels catets és igual a tres quartes partes de la de l'altre. Calculeu l'àrea del triangle.

Solució:
Anomenem $x$ al catet més llarg, llavors la longitud de l'altre ve donada per
    $\dfrac{3}{4}\,x$
i la longitud de la hipotenusa per ( teorema de Pitàgores)
    $\sqrt{x^2+\Big(\dfrac{3}{4}\,x\Big)^2}$
és a dir
    $\sqrt{\Big(\dfrac{25}{16}\,x\Big)^2}$
que és igual a
    $\dfrac{5}{4}\,x$
per tant, d'acord amb l'enunciat, podem escriure
    $x+\dfrac{3}{4}\,x +\dfrac{5}{4}\,x=24$
sumant els termes semblants del primer membre queda
    $\dfrac{12}{4}\,x=24$
    $3\,x=24$
i d'aquí
    $x=8 \,\text{cm}$
Llavors l'altre catet, la longitud del quals és igual a tres quartes parts de la d'aquest, mesura $x=6 \, \text{cm}$

Calculem, ara, l'àrea $\mathcal{A}$ del triangle rectangle; per això, prenem com a base un dels catets, llavors l'altura corresponent és la longitud de l'altre catet, per tant
      $\mathcal{A}=\dfrac{1}{2}\,(8\cdot 6) = 24 \, \text{m}^2$
i hem acabat.
$\square$

Ordenando fracciones ...

Enunciat:
Ordeneu els següents nombres racionals sense fer ús de la seva expressió decimal
                                          $\{\dfrac{4}{5}\,,\,\dfrac{13}{20}\,,\,\dfrac{3}{4}\}$

Solució:
Per establir l'ordenació procedirem de la manera següent:
  1r pas: trobarem una fracció equivalent de cada una de les donades, de tal manera que totes tres tinguin el mateix denominador ( reducció a comú denominador )
  2n pas: fet això, tan sols quedarà comparar els numeradors; l'ordre dels numeradors és el mateix que el de les fraccions amplificades.

Per reduir a comú denominador, calculem un múltiple comú dels tres denominadors, que serà el denominador comú. Els nous numeradors els calcularem multiplicant pel mateix nombre enter que multipliquem el denominador original per obtenir el múltiple comú. ( Nota: per bé que val qualsevol múltiple comú, és natural que calculem el més petit ( mínim comú múltiple ).

El mínim comú múltiple dels denominadors és
      $\text{m.c.m}(5,20,4)=20$
Llavors, ajustant convenientment els numeradors arribem a
      $\dfrac{4}{5} = \dfrac{4 \cdot (20 \div 5)}{20}= \dfrac{16}{20}$
      $\dfrac{3}{4} = \dfrac{3 \cdot (20 \div 4)}{20}= \dfrac{15}{20}$
      $13/20$   ( ja té el denominador comú: no cal fer res )
Veiem que l'odre dels numeradors és
      $13 \prec 15 \prec 20$
que ens indica l'ordre de les fraccions reduïdes a comú denominador
      $\dfrac{13}{20} \prec \dfrac{15}{20} \prec \dfrac{16}{20}$
i, tenint en compte les equivalències, arribem al resultat demanat:
      $\dfrac{13}{20} \prec \dfrac{3}{4} \prec \dfrac{4}{5}$
$\square$

Las longitudes de los lados de un cierto triángulo rectángulo que corresponden a una terna pitagórica ...

Enunciat:
Les longituds dels costats d'un triangle són $6 \, \text{dm}$, $8 \, \text{dm}$ i $10 \, \text{dm}$. Quin tipus de triangle és ?.

Solució:
Observem que el conjunt dels tres nombres que corresponen a les longituds dels costats $(6,8,10)$ és una terna pitagòrica; en efecte, $10^2$ ( que és $100$ ) és igual a la suma de $8^2$ ( que és $64$ ) i $6^2$ ( que és $36$ ), per tant el triangle donat és un triangle rectangle ( l'angle que formen els dos costats més curts és de $90^{\circ}$ ). $\square$

Diseñar una estrategia de cálculo

Enunciado:
Diseñar una estrategia de cálculo para encontrar el resultado de la siguiente operación
    $28\cdot 43$

Solución:
    $28 \cdot 43$
      $=(25+3) \cdot 43$
      $=25\cdot 43 + 3\cdot 43$
      $=43 \cdot 100 \div 2 \div 2+3\cdot 43$
      $=4300 \div 2 \div 2 + 129$
      $=2150 \div 2+129$
      $=1075+129$
      $=1075+130-1$
      $=1205-1$
      $=1204$
$\square$

[nota del autor]

Diseñar una estrategia de cálculo ...

Enunciado:
Diseñar una estrategia de cálculo mental para llegar al resultado de la siguiente operación
    $0,52 \div 0,026$

Solución:
    $0,52 \div 0,026$
      $=( 0,52 \cdot 1000) \div ( 0,026 \cdot 1000)$
      $=520 \div 26$
      $=10\cdot 2 \cdot 26 \div 26$
      $=10\cdot 2 \cdot 1$
      $=20$
$\square$

[nota del autor]

Valorar la expresión algebraica ...

Enunciado:
Valorar la expresión algebraica
    $4\,\bigg(x^2-\dfrac{2}{3}\,x\bigg)$
si $x$ toma el valor $-1$

Solución:
    $4\,\bigg[x^2-\dfrac{2}{3}\,x\bigg]_{x=-1}=4\cdot \bigg((-1)^2-\dfrac{2}{3}\cdot (-1)\bigg)$
                                    $=4\cdot \big(1+\dfrac{2}{3}\big)$
                                    $=4\cdot \big(\dfrac{5}{3}\big)$
                                    $=\dfrac{4\cdot 5}{3}$
                                    $=\dfrac{20}{3}$
$\square$

Aplicar el Teorema de Tales

Enunciado:
Calcular el valor de $x$

Solución:
Por el Teorema de Tales, podemos escribir
    $\dfrac{x}{4}=\dfrac{2}{5}$
esto es
    $\dfrac{x}{2}=\dfrac{4}{5}$
de donde
    $5\,x=4\cdot 2$
y por tanto
    $5\,x=8 \Rightarrow x=\dfrac{8}{5}$
$\square$

Aplicar el Teorema de Tales para calcular el valor de $x$

Enunciado:
Calcular el valor de $x$

Solución:
Por el el Teorema de Tales, podemos escribir
    $\dfrac{x}{5}=\dfrac{3}{6}$
que es lo mismo que
    $\dfrac{x}{3}=\dfrac{5}{6}$
por tanto
    $6\,x=3\cdot 5$
y, resolviendo la ecuación
    $6\,x=15 \Rightarrow x=\dfrac{15}{6}=\dfrac{5}{2}$
$\square$

Dados los triángulos semejantes ...

Enunciat:
Considerant els triangles semblants de la figura ( els angles homòlegs són iguals i, per tant, els costats corresponents són proporcionals ), calculeu el valor de la raó de semblança, $r$, i les longituds dels costats $a$ i $b'$.

Solució:
La raó aritmètica de les longituds dels costats corresponents dels quals en donen la seva mesura permet escriure la raó de semblança, que és igual a
    $\dfrac{306}{612}$
que, simplficant, queda
    $r=\dfrac{1}{2}$
Llavors s'ha de complir també que
    $\dfrac{b'}{268}=r$
és a dir
    $\dfrac{b'}{268}=\dfrac{1}{2} \Rightarrow b'=\dfrac{268}{2}=134\, \text{mm}$
I, semblantment, podem escriure
    $\dfrac{300}{a}=r$
és a dir
    $\dfrac{300}{a}=\dfrac{1}{2} \Rightarrow a=300\cdot 2 = 600 \, \text{mm}$
$\square$

El precio de veta al público de unos pantalones ...

Enunciat:
El preu de venda al públic d'un pantalons, inclòs el $21\,\%$ d'IVA, és de $60,00 \, \text{euros}$. Quin és el preu sense IVA ?.

Solució:
Per resoldre aquest problema cal entendre que apareixen en escena dues magnituds proporcionals: el preu de venda al públic ( que incorpora l'IVA ), que anomenarem $\mathcal{V}$, i, el preu nominal, que anomenarem $\mathcal{N}$. Aquest problema és de proporcionalitat directa perquè és evident que si el preu nominal de l'article agumenta, el preu de venda al públic també augmenta. Llavors, si $v_1$ i $v_2$ són dos valors de la magnitud $\mathcal{V}$, i $n_1$ i $n_2$ són els dos valors respectius de la magnitutd $\mathcal{N}$, s'ha de complir la següent proporció ( igualtat entre dues raons aritmètiques ) directa:
    $\dfrac{n_1}{v_1}=\dfrac{n_2}{v_2}$
        Remarca:   És important que ens fixem bé en el següent detall: els dos valors de $\mathcal{N}$ figuren als numeradors i els dos valors respectius de $\mathcal{V}$ als denominadors ( de forma equivalent, també podríem posar els dos valors de $\mathcal{N}$ als denominadors i els dos valors respectius de $\mathcal{V}$ als numeradors ).

Ara, posant els valors donats a l'enunciat, que són:
  $n_1=100$
  $v_1=100+21=121$
  $n_2=\text{?}$
  $v_2=60$
haurem de resoldre aquesta equació
    $\dfrac{100}{121}=\dfrac{n_2}{60,00}$
llavors, multiplicant ambdós membres de l'equació per $60$ arribem a
    $n_2 = \dfrac{60\cdot 100}{121}$
        $\approx 49,59 \, \text{euro}$

$\square$