martes, 14 de junio de 2016
Estadística descriptiva de una variable
ENUNCIADO. Calcular la moda, la media y la mediana de siguiente conjunto de datos tomados de una cierta variable estadística $X$:
$$\{1,2,3,4,1,4,3,2,1,1,2,3,3,2,1,2,3,2,2\}$$
SOLUCIÓN. El número de datos es $N=19$. Como hay pocos datos, podemos prescindir de elaborar la tabla de frecuencias y ordenarlos sin más: $$\{1,1,1,1,1,2,2,2,2,2,2,2,3,3,3,3,3,4,4\}$$ con lo cual es claro que el valor central ( la mediana ) es $2$; el dato que aparece con mayor frecuencia es, también, $2$ ( la moda es $2$ ), y la media, $\bar{x}$, es igual a la razón entre la suma de todos los datos ( valores de la variable estadística ) y el número de valores, por tanto $$\bar{x}=\dfrac{1\cdot 5+2\cdot 7+ 3\cdot 5 + 4 \cdot 2}{19}=\dfrac{42}{19}\approx 2,2$$
$\square$
$$\{1,2,3,4,1,4,3,2,1,1,2,3,3,2,1,2,3,2,2\}$$
SOLUCIÓN. El número de datos es $N=19$. Como hay pocos datos, podemos prescindir de elaborar la tabla de frecuencias y ordenarlos sin más: $$\{1,1,1,1,1,2,2,2,2,2,2,2,3,3,3,3,3,4,4\}$$ con lo cual es claro que el valor central ( la mediana ) es $2$; el dato que aparece con mayor frecuencia es, también, $2$ ( la moda es $2$ ), y la media, $\bar{x}$, es igual a la razón entre la suma de todos los datos ( valores de la variable estadística ) y el número de valores, por tanto $$\bar{x}=\dfrac{1\cdot 5+2\cdot 7+ 3\cdot 5 + 4 \cdot 2}{19}=\dfrac{42}{19}\approx 2,2$$
$\square$
Ecuaciones de primer grado
ENUNCIADO. Resolver las siguientes ecuaciones:
a) $3\,(1-x)=4\,(x+4)$
b) $\dfrac{5}{x}=\dfrac{2}{3+x}$
SOLUCIÓN.
a)
$3\,(1-x)=4\,(x+4)$
$3\cdot 1 -3\, x=4\,x+4\cdot 4$
$3 -3\, x=4\,x+16$
$3 -16=4\,x+3\,x$
$-13=7\,x$
$x=\dfrac{-13}{7}=-\dfrac{13}{7}$
b)
$\dfrac{5}{x}=\dfrac{2}{3+x}$
$5\cdot (3+x)=2\,x$
$5\cdot 3+5\,x=2\,x$
$15+5\,x=2\,x$
$5\,x-2\,x=-15$
$3\,x=-15$
$x=\dfrac{-15}{3}=-\dfrac{15}{3}=-5$
$\square$
a) $3\,(1-x)=4\,(x+4)$
b) $\dfrac{5}{x}=\dfrac{2}{3+x}$
SOLUCIÓN.
a)
$3\,(1-x)=4\,(x+4)$
$3\cdot 1 -3\, x=4\,x+4\cdot 4$
$3 -3\, x=4\,x+16$
$3 -16=4\,x+3\,x$
$-13=7\,x$
$x=\dfrac{-13}{7}=-\dfrac{13}{7}$
b)
$\dfrac{5}{x}=\dfrac{2}{3+x}$
$5\cdot (3+x)=2\,x$
$5\cdot 3+5\,x=2\,x$
$15+5\,x=2\,x$
$5\,x-2\,x=-15$
$3\,x=-15$
$x=\dfrac{-15}{3}=-\dfrac{15}{3}=-5$
$\square$
Cuerpos en el espacio
ENUNCIADO. Un depósito de agua tiene forma de ortoedro ( prisma recto de base rectangular ). Las medidas interiores ( longitudes de las aristas ) del depósito son: $2$, $3$ y $4$ metros, respectivamente. Se pide:
a) Dibujar una figura esquemática del depósito y anotar en ella las medidas
b) Calcular la capacidad del depósito, expresada en litros
c) Calcular la longitud de la diagonal del prisma
d) ¿ Cuánto tiempo tardará en vaciarse el depósito ( lleno ) mediante una conducción de agua, que lleva un caudal de $2 \; \dfrac{\text{L}}{\text{min}}$ ?
SOLUCIÓN.
a)
b)
El volumen del depósito es igual a $V=2 \cdot 3 \cdot 4 = 24 \; \text{m^2} = 24\,000\; \text{dm}^3$
c)
Como $1 \; \text{dm}^3$ equivale a $1 \; \text{L}$ de capacidad, la capacidad del depósito es de $24\,000 \; \text{L}$
d)
Para calcular la diagonal del ortoedro ( dibujada en rojo ) debemos tener en cuenta los dos triángulos rectángulos que se configuran ( aparecen sombreados en la figura ), entonces llamando $d$ a la diagonal del ortoedro y $\ell$ a la diagonal de la cara de la base, podemos escribir $d^2=\ell^2+3 ^2 \quad \quad (1)$ ( por el teorema de Pitágoras aplicado al triángulo sombreado de marrón ); y, aplicando el mismo teorema al triángulo sombreado en azul, $\ell^2=2^2+4^2 \quad \quad (2)$. Sustituyendo (2) en (1) resulta $d^2=2^2+3^2+4^2$, y por tanto $d=\sqrt{2^2+3^2+4^2}=\sqrt{29}\; \text{m}$
e)
Denotando por $t$ al tiempo pedido y planteando la siguiente proporción directa: $\dfrac{1}{2}=\dfrac{t}{24\,000}$, de donde despejando $t$, obtenemos $$t=12\,000\; \text{min}=200\;\text{h}=8\;\text{días}\;8\;\text{h}$$
$\square$
a) Dibujar una figura esquemática del depósito y anotar en ella las medidas
b) Calcular la capacidad del depósito, expresada en litros
c) Calcular la longitud de la diagonal del prisma
d) ¿ Cuánto tiempo tardará en vaciarse el depósito ( lleno ) mediante una conducción de agua, que lleva un caudal de $2 \; \dfrac{\text{L}}{\text{min}}$ ?
SOLUCIÓN.
a)
b)
El volumen del depósito es igual a $V=2 \cdot 3 \cdot 4 = 24 \; \text{m^2} = 24\,000\; \text{dm}^3$
c)
Como $1 \; \text{dm}^3$ equivale a $1 \; \text{L}$ de capacidad, la capacidad del depósito es de $24\,000 \; \text{L}$
d)
Para calcular la diagonal del ortoedro ( dibujada en rojo ) debemos tener en cuenta los dos triángulos rectángulos que se configuran ( aparecen sombreados en la figura ), entonces llamando $d$ a la diagonal del ortoedro y $\ell$ a la diagonal de la cara de la base, podemos escribir $d^2=\ell^2+3 ^2 \quad \quad (1)$ ( por el teorema de Pitágoras aplicado al triángulo sombreado de marrón ); y, aplicando el mismo teorema al triángulo sombreado en azul, $\ell^2=2^2+4^2 \quad \quad (2)$. Sustituyendo (2) en (1) resulta $d^2=2^2+3^2+4^2$, y por tanto $d=\sqrt{2^2+3^2+4^2}=\sqrt{29}\; \text{m}$
e)
Denotando por $t$ al tiempo pedido y planteando la siguiente proporción directa: $\dfrac{1}{2}=\dfrac{t}{24\,000}$, de donde despejando $t$, obtenemos $$t=12\,000\; \text{min}=200\;\text{h}=8\;\text{días}\;8\;\text{h}$$
$\square$
Área de un cuadrado inscrito en una circunferencia de radio dado
ENUNCIADO. Calcular el área y el perímetro de un cuadrado inscrito en una circunferencia de $5$ centímetros de radio. ¿ Cuál es el área de uno de los cuatro segmentos circulares delimitados por la circunferencia y los lados del cuadrado ?
SOLUCIÓN.
Procedimiento I:
El cuadrado inscrito en la circunferencia se divide en ocho triángulos rectángulos isósceles. La hipotenusa de cada uno de esos triángulos rectángulos isósceles es igual al radio de la circunferencia y por tanto mide $5$ centímetros. Llamemos $\ell$ a la longitud de sus catetos ( que son iguales ). El área de uno de dichos triángulos rectángulos isósceles ( de color marrón en la figura ) es igual a $\dfrac{1}{2}\,\ell\cdot \ell$, por lo tanto, el área del cuadrado es $\mathcal{A}=8\cdot ( \dfrac{1}{2}\,\ell\cdot \ell )= 4\,\ell^2 \quad \quad (1)$.
Es necesario, pues, calcular el valor de $\ell$; por el teorema de Pitágoras, $5^2=\ell^2+\ell^2$, esto es, $2\,\ell^2 \cdot 5^2$, luego $\ell^2=\dfrac{5^2}{2}$. Y sustituyendo este resultado en (1) resulta $\mathcal{A}= 4\cdot \dfrac{5^2}{2}=2\cdot 25 = 50\; \text{cm}^2$
Procedimiento II:
Otra manera de resolverlo, más sencilla, consiste en fijarnos en el triángulo rectángulo isósceles cuyos catetos son igual al radio ( $5\,\text{cm}$ ) y que en la figura está sombreado en azul. El área de uno de esos triángulos rectángulos isósceles es igual a $\dfrac{1}{2}\,5 \cdot 5 = \dfrac{25}{2}\; \text{cm}^2$; y, como el cuadrado se divide en cuatro de esos triángulos rectángulos isósceles, el área del mismo es $\mathcal{A}= 4 \cdot \dfrac{25}{2} = 2 \cdot 25 = 50 \; \text{cm}^2$
$\square$
SOLUCIÓN.
Procedimiento I:
El cuadrado inscrito en la circunferencia se divide en ocho triángulos rectángulos isósceles. La hipotenusa de cada uno de esos triángulos rectángulos isósceles es igual al radio de la circunferencia y por tanto mide $5$ centímetros. Llamemos $\ell$ a la longitud de sus catetos ( que son iguales ). El área de uno de dichos triángulos rectángulos isósceles ( de color marrón en la figura ) es igual a $\dfrac{1}{2}\,\ell\cdot \ell$, por lo tanto, el área del cuadrado es $\mathcal{A}=8\cdot ( \dfrac{1}{2}\,\ell\cdot \ell )= 4\,\ell^2 \quad \quad (1)$.
Es necesario, pues, calcular el valor de $\ell$; por el teorema de Pitágoras, $5^2=\ell^2+\ell^2$, esto es, $2\,\ell^2 \cdot 5^2$, luego $\ell^2=\dfrac{5^2}{2}$. Y sustituyendo este resultado en (1) resulta $\mathcal{A}= 4\cdot \dfrac{5^2}{2}=2\cdot 25 = 50\; \text{cm}^2$
Procedimiento II:
Otra manera de resolverlo, más sencilla, consiste en fijarnos en el triángulo rectángulo isósceles cuyos catetos son igual al radio ( $5\,\text{cm}$ ) y que en la figura está sombreado en azul. El área de uno de esos triángulos rectángulos isósceles es igual a $\dfrac{1}{2}\,5 \cdot 5 = \dfrac{25}{2}\; \text{cm}^2$; y, como el cuadrado se divide en cuatro de esos triángulos rectángulos isósceles, el área del mismo es $\mathcal{A}= 4 \cdot \dfrac{25}{2} = 2 \cdot 25 = 50 \; \text{cm}^2$
$\square$
Área y perímetro de un sector circular
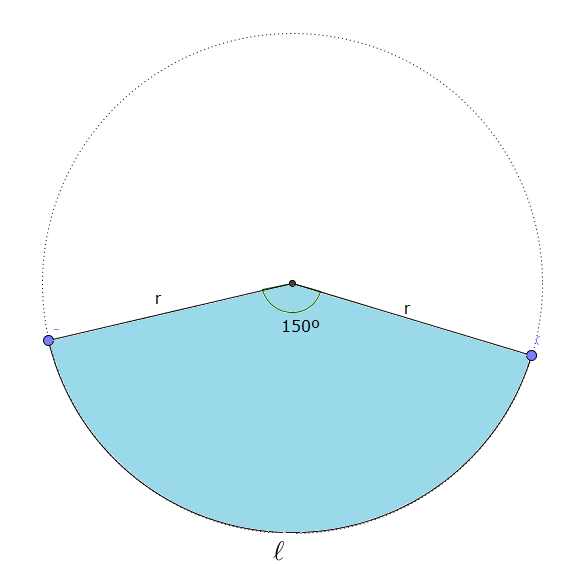
ENUNCIADO. Calcular el perímetro y el área de un sector circular de $150^{\circ}$ de amplitud angular, y de radio igual a $10$ centímetros.
SOLUCIÓN.
El área del círculo completo es igual a $\pi\cdot 10^2 = 100\,\pi\; \text{cm}^2$ y el perímetro es igual a $2\cdot\pi\cdot 10=20\,\pi\;\text{cm}$. Como, en un sector circular, ambas magnitudes son proporcionales al ángulo central de dicho sector, $$\dfrac{ \mathcal{A}_\text{sector}}{150^{\circ}}=\dfrac{100\,\pi}{360^{\circ}}\Rightarrow \mathcal{A}_\text{sector}=\dfrac{150}{360}\cdot 100\,\pi=\dfrac{5}{12}\cdot 100\,\pi=\dfrac{125}{3}\,\pi\; \text{cm}^2 \approx 131\;\text{cm}^2$$
La longitud del arco del sector circular se calcula también mediante una proporción similar:$$\dfrac{ \ell_\text{arco}}{150^{\circ}}=\dfrac{20\,\pi}{360^{\circ}}\Rightarrow \ell_{\text{arco}}=\dfrac{150}{360}\cdot 20\,\pi=\dfrac{25}{3}\,\pi\; \text{cm} \approx 26\;\text{cm}$$ por lo tanto, y añadiendo la longitud de los dos radios, resulta que el perímetro del sector es igual a $$\mathcal{P}_{\text{sector}}=\ell+2\,r=\dfrac{25}{3}\,\pi+2\cdot 10=\dfrac{25}{3}\,\pi+20\; \text{cm} \approx 46\;\text{cm}$$
$\square$
SOLUCIÓN.
El área del círculo completo es igual a $\pi\cdot 10^2 = 100\,\pi\; \text{cm}^2$ y el perímetro es igual a $2\cdot\pi\cdot 10=20\,\pi\;\text{cm}$. Como, en un sector circular, ambas magnitudes son proporcionales al ángulo central de dicho sector, $$\dfrac{ \mathcal{A}_\text{sector}}{150^{\circ}}=\dfrac{100\,\pi}{360^{\circ}}\Rightarrow \mathcal{A}_\text{sector}=\dfrac{150}{360}\cdot 100\,\pi=\dfrac{5}{12}\cdot 100\,\pi=\dfrac{125}{3}\,\pi\; \text{cm}^2 \approx 131\;\text{cm}^2$$
La longitud del arco del sector circular se calcula también mediante una proporción similar:$$\dfrac{ \ell_\text{arco}}{150^{\circ}}=\dfrac{20\,\pi}{360^{\circ}}\Rightarrow \ell_{\text{arco}}=\dfrac{150}{360}\cdot 20\,\pi=\dfrac{25}{3}\,\pi\; \text{cm} \approx 26\;\text{cm}$$ por lo tanto, y añadiendo la longitud de los dos radios, resulta que el perímetro del sector es igual a $$\mathcal{P}_{\text{sector}}=\ell+2\,r=\dfrac{25}{3}\,\pi+2\cdot 10=\dfrac{25}{3}\,\pi+20\; \text{cm} \approx 46\;\text{cm}$$
$\square$
Figuras semejantes
ENUNCIADO. Las medidas de un sobre son $10 \times 6$ centímetros. ¿ Cuáles son las medidas de otro sobre semejante al anterior, pero cuya área sea el doble de la de aquel ?.
SOLUCIÓN.
El área del primer sobre vale $10\cdot 6=60\; \text{cm}^2$, luego el área del segundo sobre es de $2 \cdot 60 = 120 \; \text{cm}^2$. La razón de semejanza es igual a la raíz cuadrada de la razón aritmética de las áreas de los dos sobres $r=\sqrt{\dfrac{120}{60}}=\sqrt{2}$.
Por tanto, el lado del segundo sobre que corresponde al de $10$ centímetros de longitud del primero es igual a $10 \cdot \sqrt{2} \approx 14,1 \; \text{cm}$; y la longitud del otro lado es igual a $6 \cdot \sqrt{2} \approx 8,5 \; \text{cm}$.
Las medidas del segundo sobre son, por tanto, $14,1 \times 8,5$ centímetros. $\square$
SOLUCIÓN.
El área del primer sobre vale $10\cdot 6=60\; \text{cm}^2$, luego el área del segundo sobre es de $2 \cdot 60 = 120 \; \text{cm}^2$. La razón de semejanza es igual a la raíz cuadrada de la razón aritmética de las áreas de los dos sobres $r=\sqrt{\dfrac{120}{60}}=\sqrt{2}$.
Por tanto, el lado del segundo sobre que corresponde al de $10$ centímetros de longitud del primero es igual a $10 \cdot \sqrt{2} \approx 14,1 \; \text{cm}$; y la longitud del otro lado es igual a $6 \cdot \sqrt{2} \approx 8,5 \; \text{cm}$.
Las medidas del segundo sobre son, por tanto, $14,1 \times 8,5$ centímetros. $\square$
domingo, 12 de junio de 2016
Ejercicios resueltos del examen final del tercer trimestre ( temas 11,12, 13 y 14 ), realizado del Viernes 9/06/2016
Un ejercicio sobre cuerpos de revolución. Cono.
ENUNCIADO. La generatriz de un cono mide $5$ decímetros, y el radio de la base $3$ decímetros. Se pide:
a) Dibujar una figura esquemática del cono y anotar en ella las medidas
b) Calcular el volumen del cono
c) Dibujar una figura esquemática del desarrollo plano del cono y anotar en ella las medidas que vienen dadas en el enunciado \par
d) Calcular el área lateral del cono
e) Calcular el área de la base
f) Calcular el área total del desarrollo plano del cono
g) Calcular el ángulo del trazado en el desarrollo plano de la superficie lateral del cono
SOLUCIÓN.
a)
b)
El volumen del cono viene dado por $V=\dfrac{1}{3}\,\pi\cdot r^2\cdot h \quad \quad (1)$, donde $h$ representa la altura del cono, esto es, la longitud del segmento $OQ$. Debemos, pues calcular su valor; si nos fijamos en el triángulo rectángulo $\triangle\{OPQ\}$, podemos aplicar el teorema de Pitágoras, $h^2+r^2=g^2$ ( donde $g$ indica la generatriz y $r$ el radio de la base ). Poniendo los datos del problema, $$h^2+3^2=5^2$$ luego $h^2=5^2-3^2=16$ y, por tanto, $h=\sqrt{16}=4\,\text{dm}$; con lo cual, de (1), $$V=\dfrac{1}{3}\,\pi\cdot 3^2\cdot 4=12\,\pi\;\text{dm}^3\approx 38\;\text{dm}^3$$
c)
El área lateral del cono viene dada por $\mathcal{A}_{\text{lateral}}=\pi\cdot r \cdot g$ y, poniendo los datos del problema, obtenemos $\mathcal{A}_{\text{lateral}}=15\,\pi \;\text{dm}^2\approx 47\;\text{dm}^2$
d)
El área de la base es $\mathcal{A}_{\text{base}}=\pi\cdot r^2$, y con los datos del problema obtenemos $$\mathcal{A}_{\text{base}}=\pi\cdot 3^2=9\,\pi\;\text{dm}^2 \approx 28\;\text{dm}^2$$
e)
El área total del desarrollo plano del cono es la suma del área de la base y del área lateral, luego su valor es $15\,\pi+9\,\pi=24\,\pi\;\text{dm}^2 \approx 75\;\text{dm}^2$
f)
El ángulo central del sector circular, $\alpha$, que representa el desarrollo plano de la superficie lateral del cono se calcula mediante la siguiente proporción ( entre la amplitud angular y la longitud del arco), $$\dfrac{\alpha}{2\,\pi\cdot r}=\dfrac{360^{\circ}}{2\,\pi\cdot g}$$ por lo que, despejando $\alpha$, se obtiene $$\alpha=360^{\circ}\cdot \dfrac{r}{g}$$, que con los datos del problema tiene el siguiente valor $$\alpha=360^{\circ}\cdot \dfrac{3}{5} = 216^{\circ}$$
$\square$
a) Dibujar una figura esquemática del cono y anotar en ella las medidas
b) Calcular el volumen del cono
c) Dibujar una figura esquemática del desarrollo plano del cono y anotar en ella las medidas que vienen dadas en el enunciado \par
d) Calcular el área lateral del cono
e) Calcular el área de la base
f) Calcular el área total del desarrollo plano del cono
g) Calcular el ángulo del trazado en el desarrollo plano de la superficie lateral del cono
SOLUCIÓN.
a)
b)
El volumen del cono viene dado por $V=\dfrac{1}{3}\,\pi\cdot r^2\cdot h \quad \quad (1)$, donde $h$ representa la altura del cono, esto es, la longitud del segmento $OQ$. Debemos, pues calcular su valor; si nos fijamos en el triángulo rectángulo $\triangle\{OPQ\}$, podemos aplicar el teorema de Pitágoras, $h^2+r^2=g^2$ ( donde $g$ indica la generatriz y $r$ el radio de la base ). Poniendo los datos del problema, $$h^2+3^2=5^2$$ luego $h^2=5^2-3^2=16$ y, por tanto, $h=\sqrt{16}=4\,\text{dm}$; con lo cual, de (1), $$V=\dfrac{1}{3}\,\pi\cdot 3^2\cdot 4=12\,\pi\;\text{dm}^3\approx 38\;\text{dm}^3$$
c)
El área lateral del cono viene dada por $\mathcal{A}_{\text{lateral}}=\pi\cdot r \cdot g$ y, poniendo los datos del problema, obtenemos $\mathcal{A}_{\text{lateral}}=15\,\pi \;\text{dm}^2\approx 47\;\text{dm}^2$
d)
El área de la base es $\mathcal{A}_{\text{base}}=\pi\cdot r^2$, y con los datos del problema obtenemos $$\mathcal{A}_{\text{base}}=\pi\cdot 3^2=9\,\pi\;\text{dm}^2 \approx 28\;\text{dm}^2$$
e)
El área total del desarrollo plano del cono es la suma del área de la base y del área lateral, luego su valor es $15\,\pi+9\,\pi=24\,\pi\;\text{dm}^2 \approx 75\;\text{dm}^2$
f)
El ángulo central del sector circular, $\alpha$, que representa el desarrollo plano de la superficie lateral del cono se calcula mediante la siguiente proporción ( entre la amplitud angular y la longitud del arco), $$\dfrac{\alpha}{2\,\pi\cdot r}=\dfrac{360^{\circ}}{2\,\pi\cdot g}$$ por lo que, despejando $\alpha$, se obtiene $$\alpha=360^{\circ}\cdot \dfrac{r}{g}$$, que con los datos del problema tiene el siguiente valor $$\alpha=360^{\circ}\cdot \dfrac{3}{5} = 216^{\circ}$$
$\square$
Cuerpos en el espacio. Un ejercicio sobre un ortoedro ( prisma recto de base rectangular ).
ENUNCIADO. Un depósito de agua tiene forma de prisma recto, de base rectangular. Las medidas interiores ( longitudes de las aristas ) del depósito son: $4$, $5$ y $6$ metros, respectivamente. Se pide:
a) Dibujar una figura esquemática del depósito y anotar en ella las medidas
c) Calcular la capacidad del depósito, expresada en litros
b) ¿ Cuántos cubos de $1,5$ litros de capacidad es necesario llenar para vaciarlo ?
d) Calcular la longitud de la diagonal del prisma
e) Dibujar una figura que mueste el desarrollo plano del depósito ( está abierto por la cara superior ), y anotar en ella las medidas que vienen dadas en el enunciado
f) Calcular el área total de las paredes del depósito
SOLUCIÓN. Este ejercicio es muy similar a este otro ( que ya está resuelto y comentado ). $\square$
a) Dibujar una figura esquemática del depósito y anotar en ella las medidas
c) Calcular la capacidad del depósito, expresada en litros
b) ¿ Cuántos cubos de $1,5$ litros de capacidad es necesario llenar para vaciarlo ?
d) Calcular la longitud de la diagonal del prisma
e) Dibujar una figura que mueste el desarrollo plano del depósito ( está abierto por la cara superior ), y anotar en ella las medidas que vienen dadas en el enunciado
f) Calcular el área total de las paredes del depósito
SOLUCIÓN. Este ejercicio es muy similar a este otro ( que ya está resuelto y comentado ). $\square$
Un ejercicio de aplicación del teorema de Pitágoras
ENUNCIADO. Considerar la siguiente figura:
Las longitudes de los segmentos $a$, $AD$ y $DB$ miden $4 \; \text{cm}$, $3 \; \text{cm}$ y $2 \; \text{cm}$, respectivamente. Se pide:
a) Calcular el área del triángulo $\triangle\{ABC\}$
b) Calcular el perímetro del triángulo $\triangle\{ABC\}$
SOLUCIÓN.
a)
El área del triángulo $\triangle\{ABC\}$ es igual a $\dfrac{a \cdot AD}{2}=\dfrac{4 \cdot 3}{2}=6\,\text{cm}^2$
b)
El perímetro del triángulo $\triangle\{ABC\}$ es igual a la suma de las longitudes de sus lados, $a+b+c$ y aplicando el teorema de Pitágoras a los triángulos ( rectángulos ) $\triangle\{ADC\}$ y $\triangle\{ADB\}$ obtenemos $4 +\sqrt{(4+2)^2+3^2}+\sqrt{2^2+3^2}=4+\sqrt{45}+\sqrt{13} \; \text{cm} \approx 14 \, \text{cm}$
$\square$
Las longitudes de los segmentos $a$, $AD$ y $DB$ miden $4 \; \text{cm}$, $3 \; \text{cm}$ y $2 \; \text{cm}$, respectivamente. Se pide:
a) Calcular el área del triángulo $\triangle\{ABC\}$
b) Calcular el perímetro del triángulo $\triangle\{ABC\}$
SOLUCIÓN.
a)
El área del triángulo $\triangle\{ABC\}$ es igual a $\dfrac{a \cdot AD}{2}=\dfrac{4 \cdot 3}{2}=6\,\text{cm}^2$
b)
El perímetro del triángulo $\triangle\{ABC\}$ es igual a la suma de las longitudes de sus lados, $a+b+c$ y aplicando el teorema de Pitágoras a los triángulos ( rectángulos ) $\triangle\{ADC\}$ y $\triangle\{ADB\}$ obtenemos $4 +\sqrt{(4+2)^2+3^2}+\sqrt{2^2+3^2}=4+\sqrt{45}+\sqrt{13} \; \text{cm} \approx 14 \, \text{cm}$
$\square$
Un ejercicio de aplicación del teorema de Tales
ENUNCIADO. Las rectas $r$, $s$ y $t$ de la figura son paralelas. Hallar $x$ e $y$.
SOLUCIÓN.
Nota: los datos del problema, así como los resultados, vienen expresadas en unidades arbitrarias de longitud
Por el teorema de Tales podemos escribir: $$\dfrac{2}{3}=\dfrac{x}{5}$$ y despejando $x$, $$x=\dfrac{2\cdot 5}{3}=\dfrac{10}{3} \approx 3,33$$ de manera análoga, para el el último par de segmentos interceptados $$\dfrac{2}{3}=\dfrac{1,5}{y}$$ luego $$2\,y=1,5 \cdot 3$$ y despejando $y$ obtenemos $$y=\dfrac{1,5\cdot 3}{2}=2,25$$
$\square$
SOLUCIÓN.
Nota: los datos del problema, así como los resultados, vienen expresadas en unidades arbitrarias de longitud
Por el teorema de Tales podemos escribir: $$\dfrac{2}{3}=\dfrac{x}{5}$$ y despejando $x$, $$x=\dfrac{2\cdot 5}{3}=\dfrac{10}{3} \approx 3,33$$ de manera análoga, para el el último par de segmentos interceptados $$\dfrac{2}{3}=\dfrac{1,5}{y}$$ luego $$2\,y=1,5 \cdot 3$$ y despejando $y$ obtenemos $$y=\dfrac{1,5\cdot 3}{2}=2,25$$
$\square$
martes, 7 de junio de 2016
Poliedros no convexos que no cumplen la propiedad de Euler
La propiedad de Euler sobre los poliedros ( $v-a+c=2$, donde $v$ denota el número de vértices; $a$, el número de aristas; y $c$, el número de caras ) es válida para todo poliedro convexo; ahora bien, existen poliedros no convexos que también la cumplen; por ejemplo, un prisma cuya base tenga forma de "L". Por supuesto, los hay ( no convexos ) que no la cumplen, aunque a veces cuesta dar con alguno -- el otro día, en clase, me pasó eso: no daba con ninguno --. Uno de estos poliedros ( ya tengo unos cuántos para mostrar ) es un prisma con un agujero ciego, con el mismo contorno de la base, tal como se muestra en la siguiente figura
Los hay, también, que son muy complicados, como por ejemplo el poliedro de Szászár ( fuente: Wikipedia ). Siguiendo el enlace podréis echarle un vistazo.
Los hay, también, que son muy complicados, como por ejemplo el poliedro de Szászár ( fuente: Wikipedia ). Siguiendo el enlace podréis echarle un vistazo.
Suscribirse a:
Entradas (Atom)