Área y perímetro de un sector circular

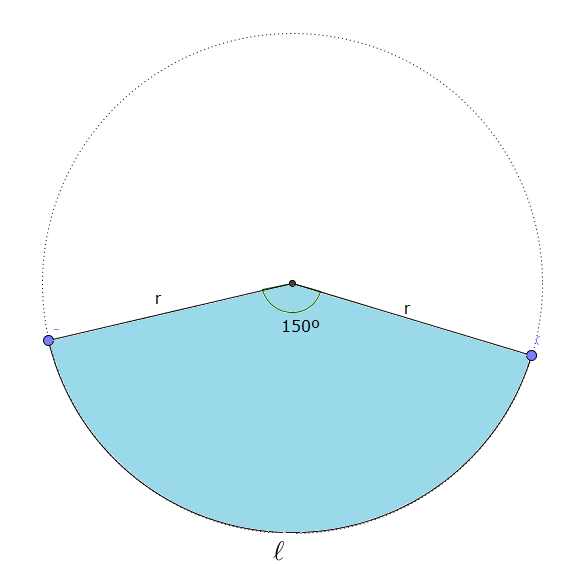
ENUNCIADO. Calcular el perímetro y el área de un sector circular de $150^{\circ}$ de amplitud angular, y de radio igual a $10$ centímetros.

SOLUCIÓN.
El área del círculo completo es igual a $\pi\cdot 10^2 = 100\,\pi\; \text{cm}^2$ y el perímetro es igual a $2\cdot\pi\cdot 10=20\,\pi\;\text{cm}$. Como, en un sector circular, ambas magnitudes son proporcionales al ángulo central de dicho sector, $$\dfrac{ \mathcal{A}_\text{sector}}{150^{\circ}}=\dfrac{100\,\pi}{360^{\circ}}\Rightarrow \mathcal{A}_\text{sector}=\dfrac{150}{360}\cdot 100\,\pi=\dfrac{5}{12}\cdot 100\,\pi=\dfrac{125}{3}\,\pi\; \text{cm}^2 \approx 131\;\text{cm}^2$$

La longitud del arco del sector circular se calcula también mediante una proporción similar:$$\dfrac{ \ell_\text{arco}}{150^{\circ}}=\dfrac{20\,\pi}{360^{\circ}}\Rightarrow \ell_{\text{arco}}=\dfrac{150}{360}\cdot 20\,\pi=\dfrac{25}{3}\,\pi\; \text{cm} \approx 26\;\text{cm}$$ por lo tanto, y añadiendo la longitud de los dos radios, resulta que el perímetro del sector es igual a $$\mathcal{P}_{\text{sector}}=\ell+2\,r=\dfrac{25}{3}\,\pi+2\cdot 10=\dfrac{25}{3}\,\pi+20\; \text{cm} \approx 46\;\text{cm}$$

$\square$